题目内容
在△ABC所在平面存在一点O使得
+
+
=
,则面积
=______.
| OA |
| OB |
| OC |
| 0 |
| S△OBC |
| S△ABC |
∵
+
+
=
,
∴
+
=
,
设
+
=
∴O是AD的中点,
要求面积之比的两个三角形是同底的三角形,
∴面积之比等于三角形的高之比,
∴比值是
,
故答案为:
.
| OA |
| OB |
| OC |
| 0 |
∴
| OB |
| OC |
| AO |
设
| OB |
| OC |
| OD |
∴O是AD的中点,
要求面积之比的两个三角形是同底的三角形,
∴面积之比等于三角形的高之比,
∴比值是
| 1 |
| 3 |
故答案为:
| 1 |
| 3 |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
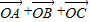 =
=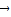 ,则面积
,则面积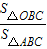 = .
= .