题目内容
在△ABC所在平面存在一点O使得| OA |
| OB |
| OC |
| 0 |
| S△OBC |
| S△ABC |
分析：三个向量之间的关系是和为零向量，移项得到两个向量的和与一个向量之间的关系，根据平行四边形法则得到三等分点，又有两个三角形是同底的三角形，得到面积之比．
解答：解：∵
+
+
=
，
∴
+
=
，
设
+
=
∴O是AD的中点，
要求面积之比的两个三角形是同底的三角形，
∴面积之比等于三角形的高之比，
∴比值是
，
故答案为：
．
| OA |
| OB |
| OC |
| 0 |
∴
| OB |
| OC |
| AO |
设
| OB |
| OC |
| OD |
∴O是AD的中点，
要求面积之比的两个三角形是同底的三角形，
∴面积之比等于三角形的高之比，
∴比值是
| 1 |
| 3 |
故答案为：
| 1 |
| 3 |
点评：用一组向量来表示一个向量，是以后解题过程中常见到的，向量的加减运算是用向量解决问题的基础，要学好运算，才能用向量解决立体几何问题，三角函数问题，好多问题都是以向量为载体．
练习册系列答案
时刻准备着暑假作业原子能出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案
相关题目
=
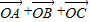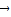，则面积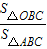
= ．