题目内容
设数列![]() 满足
满足![]() ,
,![]() ,其中
,其中![]() ,
,![]() 均为实数,且
均为实数,且![]() ,
,![]() .
.
(1)求证:数列![]() 为等比数列;
为等比数列;
(2)设![]() ,
,![]() ,
,![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() ;
;
(3)若![]() 对任意的
对任意的![]() 成立,求证:
成立,求证:![]() .
.
解:(1)由题意,![]() ,又
,又![]() , 则
, 则 ![]() …………………2分
…………………2分
![]() 所以数列
所以数列![]() 是等比数列. …………………3分
是等比数列. …………………3分
(2)由(1)得![]() ,即
,即![]()
![]() …………………4分
…………………4分
所以![]() …………………5分
…………………5分
由![]() (记为①)得:
(记为①)得:![]() (记为②)
(记为②)
![]() 得:
得:![]()
所以![]() ………………10分
………………10分
(3)由(1)知![]() ,若
,若![]() ,则
,则![]() .
.
又![]() , 故有
, 故有![]() ,由
,由![]() 得
得![]() …………………11分
…………………11分
下证![]() ,用反证法
,用反证法
法一:假设![]() 。由函数
。由函数![]() 的图象值,当
的图象值,当![]() 趋于无穷大时,
趋于无穷大时,![]() 趋于无穷大,
趋于无穷大,
![]() 不能对恒成立,导致矛盾。所以
不能对恒成立,导致矛盾。所以![]() 。
。
综上所述![]() …………………14分
…………………14分
法二:假设![]() 。 因
。 因![]() 所以
所以![]() 即
即![]() 恒成立, 又
恒成立, 又![]() 为常数, 所以
为常数, 所以![]() 不能恒成立,导致矛盾。所以
不能恒成立,导致矛盾。所以![]() 。
。
综上所述![]() …………………14分
…………………14分

练习册系列答案
相关题目
 ,
, (
( )由下列条件确定:①
)由下列条件确定:① ;②当
;②当 时,
时, 与
与 满足:当
满足:当 时,
时, ,
, ;当
;当 时,
时, ,
, .
. ,
, ,写出
,写出 ,并求数列
,并求数列 的通项公式;
的通项公式;  (
(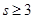 ,且
,且 ),试用
),试用 表示
表示
 ;
;
 满足
满足 ,
, ,
, (其中
(其中 为给定的不小于2的整数),求证:当
为给定的不小于2的整数),求证:当 时,恒有
时,恒有 .
.