题目内容
设数列![]() 满足
满足![]() ,
,![]() ,其中
,其中![]() .
.
(1)证明:对一切![]() ,有
,有![]() ;
;
证明 : (1)在已知关系式![]() 中,令
中,令![]() ,可得
,可得![]() ;
;
令![]() ,可得
,可得![]() ①
①
令![]() ,可得
,可得![]() ②
②
由①得![]() ,
,![]() ,
,![]() ,
,![]() ,
,
代入②,化简得![]() . ----------------------------7分
. ----------------------------7分
(2)由![]() ,得
,得![]() ,故数列
,故数列![]() 是首项为
是首项为![]() ,公差为2的等差数列,因此
,公差为2的等差数列,因此![]() .
.
于是![]() .
.
因为![]() ,所以
,所以
![]() .
.
------------------14分

练习册系列答案
相关题目
 ,
, (
( )由下列条件确定:①
)由下列条件确定:① ;②当
;②当 时,
时, 与
与 满足:当
满足:当 时,
时, ,
, ;当
;当 时,
时, ,
, .
. ,
, ,写出
,写出 ,并求数列
,并求数列 的通项公式;
的通项公式;  (
(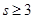 ,且
,且 ),试用
),试用 表示
表示
 ;
;
 满足
满足 ,
, ,
, (其中
(其中 为给定的不小于2的整数),求证:当
为给定的不小于2的整数),求证:当 时,恒有
时,恒有 .
.