题目内容
(14分)
在数列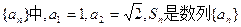 的前n项和。当
的前n项和。当 时,
时,
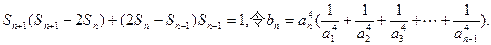
(1)求数列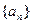 的通项公式;试用n和
的通项公式;试用n和 表示
表示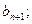
(2)若 ,证明:
,证明:
(3)当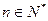 时,证明
时,证明
在数列
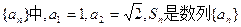 的前n项和。当
的前n项和。当 时,
时,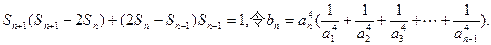
(1)求数列
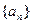 的通项公式;试用n和
的通项公式;试用n和 表示
表示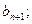
(2)若
 ,证明:
,证明:
(3)当
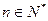 时,证明
时,证明
略
(1)证明:由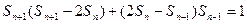
得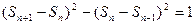 ,即
,即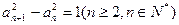
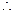 数列
数列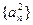 是首项为1,公差为1的等差数列
是首项为1,公差为1的等差数列
于是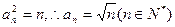 …………4分
…………4分
(2)当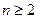 时,
时,
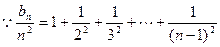
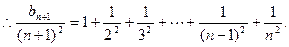
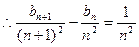
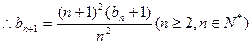 …………3分
…………3分
当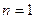 时,
时,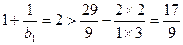 ,不等式成立;
,不等式成立;
当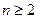 时,由(1)得
时,由(1)得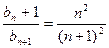
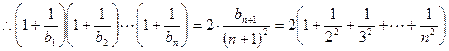
 又当
又当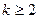 时,
时,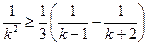
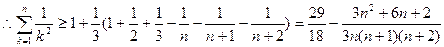
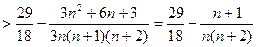
于是当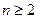 时,
时,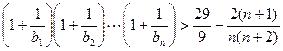
综上所述,对一切
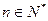 ,不等式都成立。 …………10分
,不等式都成立。 …………10分
(3)略
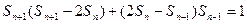
得
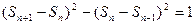 ,即
,即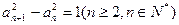
 数列
数列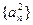 是首项为1,公差为1的等差数列
是首项为1,公差为1的等差数列于是
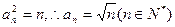 …………4分
…………4分(2)当
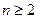 时,
时,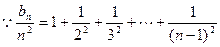
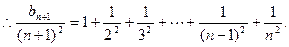
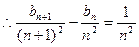
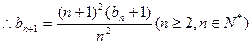 …………3分
…………3分当
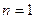 时,
时,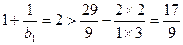 ,不等式成立;
,不等式成立;当
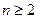 时,由(1)得
时,由(1)得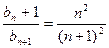
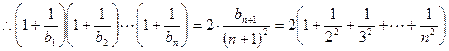
 又当
又当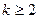 时,
时,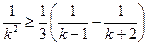
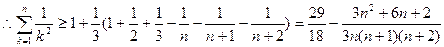
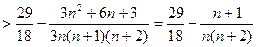
于是当
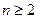 时,
时,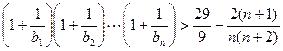
综上所述,对一切

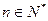 ,不等式都成立。 …………10分
,不等式都成立。 …………10分(3)略

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
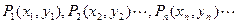 ,对一切正整数
,对一切正整数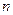 ,点
,点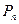 位于函数
位于函数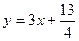 的图象上,且
的图象上,且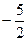 为首项,
为首项,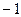 为公差的等差数列
为公差的等差数列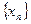 。
。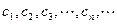 中的每一条的对称轴都垂直于
中的每一条的对称轴都垂直于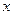 轴,第
轴,第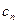 的顶点为
的顶点为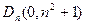 ,记与数列
,记与数列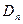 的直线的斜率为
的直线的斜率为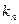 ,求:
,求: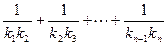 。
。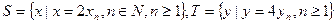 ,等差数列
,等差数列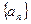 的任一项
的任一项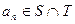 ,其中
,其中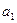 是
是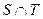 中的最大数,
中的最大数,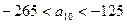 ,求
,求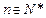 )个圆盘依其半径大小,大的在下,小的在上套在A柱上,现要将套在A柱上的盘换到C柱上,要求每次只能搬动一个,而且任何时候不允许将大盘套在小盘上面,假定有三根柱子A、B、C可供使用.
)个圆盘依其半径大小,大的在下,小的在上套在A柱上,现要将套在A柱上的盘换到C柱上,要求每次只能搬动一个,而且任何时候不允许将大盘套在小盘上面,假定有三根柱子A、B、C可供使用.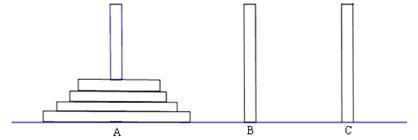
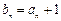 ,求和
,求和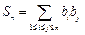 (
(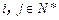 );
); 表示所有的积
表示所有的积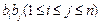 的和)
的和)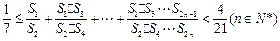 .
.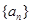 满足
满足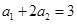 ,且对任意的
,且对任意的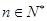 ,点
,点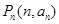 都有
都有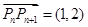 ,则
,则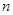 项和
项和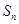 为( )
为( )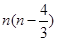
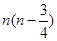
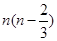
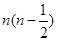
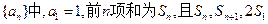 成等差数列,则
成等差数列,则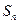 =( )
=( )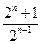
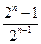
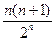
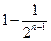
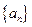 满足
满足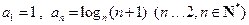 .定义:使
.定义:使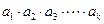 为正整数的
为正整数的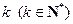 叫做“和谐数”,则在区间
叫做“和谐数”,则在区间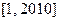 内所有的“和谐数”的和为
内所有的“和谐数”的和为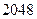
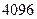
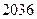
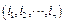 (
(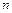 是不小于
是不小于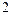 的正整数),如果在
的正整数),如果在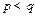 时有
时有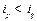 ,则称“
,则称“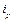 与
与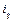 ”是该数组的一个“顺序”,一个数组中所有“顺序”的个数称为此数组的“顺序数”.例如,数组
”是该数组的一个“顺序”,一个数组中所有“顺序”的个数称为此数组的“顺序数”.例如,数组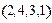 中有顺序“2,4”,“2,3”,其“顺序数”等于2.若各数互不相等的正数数组
中有顺序“2,4”,“2,3”,其“顺序数”等于2.若各数互不相等的正数数组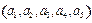 的“顺序数”是4,则
的“顺序数”是4,则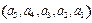 的“顺序数”是 .
的“顺序数”是 .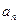 }的前
}的前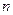 项和
项和 ,则其通项
,则其通项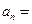 ;
;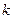 项满足
项满足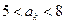 ,则
,则