题目内容
已知锐角 中的内角
中的内角 、
、 、
、 的对边分别为
的对边分别为 、
、 、
、 ,定义向量
,定义向量 ,
, ,且
,且 .
.
(1)求 的单调减区间;
的单调减区间;
(2)如果 ,求
,求 的面积的最大值.
的面积的最大值.
【答案】
(1) ;(2)
;(2)
【解析】
试题分析:(1)利用向量垂直,向的数量积为0 得到 ,根据锐角三角形的内角
,根据锐角三角形的内角 求角
求角 ,再由正弦函数
,再由正弦函数 得单调减区间为
得单调减区间为 求解;(2)由余弦定理及三角形的面积公式求解.
求解;(2)由余弦定理及三角形的面积公式求解.
试题解析:∵ ,
,
 ,
,
∴ ,∴
,∴ ,又
,又 ,∴
,∴ ,(4分)
,(4分)
(1) ,由
,由 得:
得:
函数 的单调减区间为
的单调减区间为 . (8分)
. (8分)
(2)由余弦定理知, ,
,
∴ . (12分)
. (12分)
考点:向量的数量积,二倍角公式,余弦定理,三角形的面积公式.

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目
 中,内角
中,内角 的对边分别为
的对边分别为 ,且
,且 ,
, .
. 的大小;
的大小;
 ,求
,求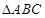 中的内角
中的内角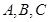 的对边分别为
的对边分别为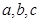 ,定义向量
,定义向量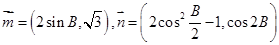 ,且
,且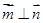 .
.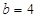 ,求
,求

 共线,且有函数
共线,且有函数
 的周期及最大值;
的周期及最大值; 中的三个内角分别为A、B、C,若有
中的三个内角分别为A、B、C,若有 ,边
,边 ,
, ,求的
,求的