题目内容
已知锐角![]() 中的内角
中的内角![]() 的对边分别为
的对边分别为![]() ,定义向量
,定义向量![]() ,且
,且![]() .
.
(Ⅰ)求角B的值;(Ⅱ)如果![]() ,求
,求![]() 的面积的最大值.
的面积的最大值.
.
解:(Ⅰ)![]() ,
,
因为![]() ,所以
,所以![]() =0,即(2sinB,
=0,即(2sinB,![]() )•(cosB,cos2B)=0,
)•(cosB,cos2B)=0,
所以2sinBcosB+![]() cos2B=sin2B+
cos2B=sin2B+![]() cos2B=2sin(2B+60°)=0,
cos2B=2sin(2B+60°)=0,
又△ABC为锐角三角形,所以2B+60°=180°,解得B=60°;
(Ⅱ)由余弦定理得,b2=a2+c2﹣2accos60°,即16=a2+c2﹣ac,
则16=a2+c2﹣ac≥2ac﹣ac=ac,当且仅当a=c时取等号,
所以△ABC的面积![]()
![]() ,
,
所以△ABC的面积的最大值是4![]() .
.

练习册系列答案
 举一反三期末百分冲刺卷系列答案 举一反三期末百分冲刺卷系列答案
相关题目
|
 中,内角
中,内角 的对边分别为
的对边分别为 ,且
,且 ,
, .
. 的大小;
的大小;
 ,求
,求 中的内角
中的内角 、
、 、
、 的对边分别为
的对边分别为 、
、 、
、 ,定义向量
,定义向量 ,
, ,且
,且 .
. 的单调减区间;
的单调减区间; ,求
,求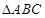 中的内角
中的内角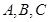 的对边分别为
的对边分别为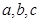 ,定义向量
,定义向量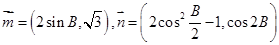 ,且
,且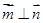 .
.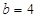 ,求
,求 中内角
中内角 、
、 、
、 的对边分别为
的对边分别为 、
、 、
、 ,
, ,且
,且 .
. ,
, 图象上相邻两最高点间的距离为
图象上相邻两最高点间的距离为 ,求
,求 的取值范围
的取值范围