题目内容
已知圆的方程为x2+y2=1,把圆上各点的横坐标伸长到原来的2倍,纵坐标不变,得到一椭圆,则以该椭圆的焦点为顶点、顶点为焦点的双曲线方程为
- A.

- B.

- C.

- D.
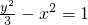
A
分析:把圆上各点的横坐标伸长到原来的2倍,纵坐标不变,得到一椭圆的方程为: ,再求出椭圆的顶点和焦点,从而得到双曲线的焦点和顶点,进而得到双曲线方程.
,再求出椭圆的顶点和焦点,从而得到双曲线的焦点和顶点,进而得到双曲线方程.
解答:把圆上各点的横坐标伸长到原来的2倍,纵坐标不变,得到一椭圆的方程为: ,
,
椭圆 的顶点为(-2,0)和(2,0),焦点为(-
的顶点为(-2,0)和(2,0),焦点为(- ,0)和(
,0)和(  ,0).
,0).
∴双曲线的焦点坐标是(-2,0)和(2,0),顶点为(- ,0)和(
,0)和(  ,0).
,0).
∴双曲线的a= ,c=2?b=1
,c=2?b=1
∴双曲线方程为 .
.
故选A.
点评:本题主要考查变换法求解曲线的方程,考查双曲线和椭圆的性质和应用,解题时要注意区分双曲线和椭圆的基本性质.
分析:把圆上各点的横坐标伸长到原来的2倍,纵坐标不变,得到一椭圆的方程为:
 ,再求出椭圆的顶点和焦点,从而得到双曲线的焦点和顶点,进而得到双曲线方程.
,再求出椭圆的顶点和焦点,从而得到双曲线的焦点和顶点,进而得到双曲线方程.解答:把圆上各点的横坐标伸长到原来的2倍,纵坐标不变,得到一椭圆的方程为:
 ,
,椭圆
 的顶点为(-2,0)和(2,0),焦点为(-
的顶点为(-2,0)和(2,0),焦点为(- ,0)和(
,0)和(  ,0).
,0).∴双曲线的焦点坐标是(-2,0)和(2,0),顶点为(-
 ,0)和(
,0)和(  ,0).
,0).∴双曲线的a=
 ,c=2?b=1
,c=2?b=1∴双曲线方程为
 .
.故选A.
点评:本题主要考查变换法求解曲线的方程,考查双曲线和椭圆的性质和应用,解题时要注意区分双曲线和椭圆的基本性质.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
已知圆的方程为x2+y2-6x-8y=0,设该圆过点(3,5)的最长弦和最短弦分别为AC和BD,则四边形ABCD的面积为( )
A、10
| ||
B、20
| ||
C、30
| ||
D、40
|
 已知圆的方程为x2+y2=4,过点M(2,4)作圆的两条切线,切点分别为A1、A2,直线A1A2恰好经过椭圆
已知圆的方程为x2+y2=4,过点M(2,4)作圆的两条切线,切点分别为A1、A2,直线A1A2恰好经过椭圆