题目内容
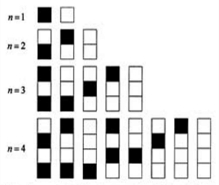 15、给n个自上而下相连的正方形着黑色或白色.当n≤4时,在所有不同的着色方案中,黑色正方形互不相连的着色方案如图所示:
15、给n个自上而下相连的正方形着黑色或白色.当n≤4时,在所有不同的着色方案中,黑色正方形互不相连的着色方案如图所示:由此推断,当n=6时,黑色正方形互不相邻的着色方案共有
21
种,至少有两个黑色正方形相邻的着色方案共有43
种,(结果用数值表示)分析:根据所给的涂色的方案,观测相互之间的方法数,得到规律,根据这个规律写出当n取不同值时的结果数;利用给小正方形涂色的所有法数减去黑色正方形互不相邻的着色方案,得到结果.
解答:解:由题意知当n=1时,有2种,
当n=2时,有3种,
当n=3时,有2+3=5种,
当n=4时,有3+5=8种,
当n=5时,有5+8=13种,
当n=6时,有8+13=21种,
当n=6时,黑色和白色的小正方形共有26种涂法,
黑色正方形互不相邻的着色方案共有21种结果,
∴至少有两个黑色正方形相邻的着色方案共有64-21=43种结果,
故答案为:21;43
当n=2时,有3种,
当n=3时,有2+3=5种,
当n=4时,有3+5=8种,
当n=5时,有5+8=13种,
当n=6时,有8+13=21种,
当n=6时,黑色和白色的小正方形共有26种涂法,
黑色正方形互不相邻的着色方案共有21种结果,
∴至少有两个黑色正方形相邻的着色方案共有64-21=43种结果,
故答案为:21;43
点评:本题考查简单的排列组合及简单应用,考查观察规律,找出结果的过程,是一个比较麻烦的题目,当作为高考题目比前几年的排列组合问题不难.

练习册系列答案
相关题目
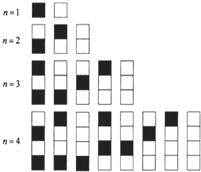 给n个自上而下相连的正方形着黑色或白色.当n≤4时,在所有不同的着色方案中,黑色正方形互不相连的着色方案如图所示:由此推断,当n=6时,黑色正方形互不相连的着色方案共有多少种,至少有两个黑色正方形相连的着色方案共有多少种?
给n个自上而下相连的正方形着黑色或白色.当n≤4时,在所有不同的着色方案中,黑色正方形互不相连的着色方案如图所示:由此推断,当n=6时,黑色正方形互不相连的着色方案共有多少种,至少有两个黑色正方形相连的着色方案共有多少种?






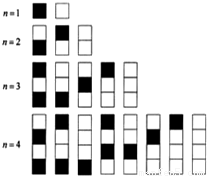 给n个自上而下相连的正方形着黑色或白色.当n≤4时,在所有不同的着色方案中,黑色正方形互不相连的着色方案如图所示:由此推断,当n=6时,黑色正方形互不相邻的着色方案共有 种,至少有两个黑色正方形相邻的着色方案共有 种,(结果用数值表示)
给n个自上而下相连的正方形着黑色或白色.当n≤4时,在所有不同的着色方案中,黑色正方形互不相连的着色方案如图所示:由此推断,当n=6时,黑色正方形互不相邻的着色方案共有 种,至少有两个黑色正方形相邻的着色方案共有 种,(结果用数值表示)