题目内容
给n个自上而下相连的正方形着黑色或白色,当n≤4时,在所有不同的着色方案中,黑色正方形互不相邻的着色方案如图1所示,由此推断,当n=6时,黑色正方形互不相邻的着色方案共有__________种,至少有两个黑色正方形相邻的着色方案共有_________.
(结果用数值表示)
n=1

n=2

n=3
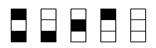
n=4

【答案】
21;43
【解析】由题意知当n=1时,有2种,
当n=2时,有3种,
当n=3时,有2+3=5种,
当n=4时,有3+5=8种,
当n=5时,有5+8=13种,
当n=6时,有8+13=21种,
当n=6时,黑色和白色的小正方形共有26种涂法,
黑色正方形互不相邻的着色方案共有21种结果,
∴至少有两个黑色正方形相邻的着色方案共有64-21=43种结果,
故答案为:21;43

练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
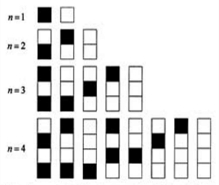 15、给n个自上而下相连的正方形着黑色或白色.当n≤4时,在所有不同的着色方案中,黑色正方形互不相连的着色方案如图所示:
15、给n个自上而下相连的正方形着黑色或白色.当n≤4时,在所有不同的着色方案中,黑色正方形互不相连的着色方案如图所示: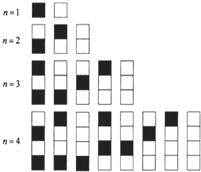 给n个自上而下相连的正方形着黑色或白色.当n≤4时,在所有不同的着色方案中,黑色正方形互不相连的着色方案如图所示:由此推断,当n=6时,黑色正方形互不相连的着色方案共有多少种,至少有两个黑色正方形相连的着色方案共有多少种?
给n个自上而下相连的正方形着黑色或白色.当n≤4时,在所有不同的着色方案中,黑色正方形互不相连的着色方案如图所示:由此推断,当n=6时,黑色正方形互不相连的着色方案共有多少种,至少有两个黑色正方形相连的着色方案共有多少种?



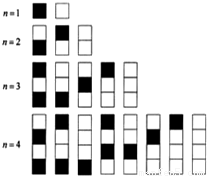 给n个自上而下相连的正方形着黑色或白色.当n≤4时,在所有不同的着色方案中,黑色正方形互不相连的着色方案如图所示:由此推断,当n=6时,黑色正方形互不相邻的着色方案共有 种,至少有两个黑色正方形相邻的着色方案共有 种,(结果用数值表示)
给n个自上而下相连的正方形着黑色或白色.当n≤4时,在所有不同的着色方案中,黑色正方形互不相连的着色方案如图所示:由此推断,当n=6时,黑色正方形互不相邻的着色方案共有 种,至少有两个黑色正方形相邻的着色方案共有 种,(结果用数值表示)