题目内容
若称 为n个正数a1+a2+…+an的“均倒数”已知数列{an}的各项均为正,且其前n项的“均倒数”为
为n个正数a1+a2+…+an的“均倒数”已知数列{an}的各项均为正,且其前n项的“均倒数”为 则数列{an}的通项公式为
则数列{an}的通项公式为
A.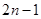 | B.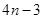 | C.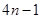 | D. |
B
解析试题分析:由题意可知前n项和 ,当
,当 时
时 ,当
,当 时
时 ,经验证
,经验证 符合,所以通项为
符合,所以通项为
考点:数列通项公式
点评:由数列前n项和 求通项
求通项 时主要利用
时主要利用 分别求出后验证最终结果能否合并
分别求出后验证最终结果能否合并

练习册系列答案
相关题目
数列 的通项公式为
的通项公式为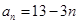 ,
,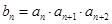 ,
, 是数列
是数列 的前
的前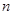 项和,则
项和,则 的最大值为( )
的最大值为( )
| A.280 | B.300 | C.310 | D.320 |
已知数列 的通项公式为
的通项公式为 ,那么满足
,那么满足 的整数
的整数 ( )
( )
| A.有3个 | B.有2个 | C.有1个 | D.不存在 |
设 ,且
,且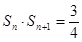 ,则
,则 的值为 ( )
的值为 ( )
| A.9 | B.8 | C.7 | D.6 |
定义:称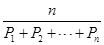 为
为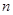 个正数
个正数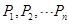 的“均倒数”.若数列
的“均倒数”.若数列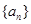 的前
的前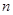 项的“均倒数”为
项的“均倒数”为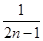 ,则数列
,则数列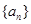 的通项公式为( )
的通项公式为( )
A.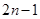 | B. | C. | D.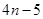 |
数列1,1+2,1+2+4,…,1+2+22+…+2n-1,…的前n项和Sn>1020,那么n的最小值是( )
| A.7 | B.8 | C.9 | D.10 |
 表示位于从上到下第
表示位于从上到下第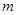 行,从左到右
行,从左到右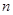 列的数,比如
列的数,比如 ,若
,若 ,则有( )
,则有( )

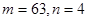
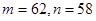
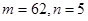
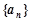 是有穷数列,且项数
是有穷数列,且项数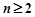 .定义一个变换
.定义一个变换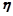 :将数列
:将数列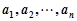 ,变成
,变成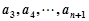 ,其中
,其中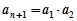 是变换所产生的一项.从数列
是变换所产生的一项.从数列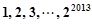 开始,反复实施变换
开始,反复实施变换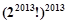
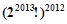
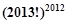
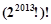
 为等差数列,若
为等差数列,若 并且他的前n项和
并且他的前n项和 有最大值,那么当
有最大值,那么当 取得最小正值时,n=( )
取得最小正值时,n=( )