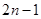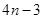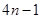题目内容
将正整数按如图所示的规律排列下去,且用 表示位于从上到下第
表示位于从上到下第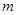 行,从左到右
行,从左到右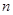 列的数,比如
列的数,比如 ,若
,若 ,则有( )
,则有( )
A. | B.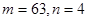 |
C.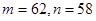 | D.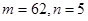 |
A
解析试题分析:前m-1行共用去1+2+3+……+(m-1)= 个数,由
个数,由
 有正整数解,得,m=63,第m-1行最后一个数是1953,所以,2013-1953=60,即n=60,故选A。
有正整数解,得,m=63,第m-1行最后一个数是1953,所以,2013-1953=60,即n=60,故选A。
考点:等差数列的求和公式
点评:中档题,解题的关键是理解 的意义及“数阵”的构成规律。
的意义及“数阵”的构成规律。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
数列 ,…前n项的和为
,…前n项的和为
A. | B. |
C. | D. |
已知数列 的通项公式为
的通项公式为
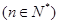 ,其前n项和为
,其前n项和为 ,则在数列
,则在数列 中,有理数项的项数为( )
中,有理数项的项数为( )
| A.42 | B.43 | C.44 | D.45 |
设 ( )
( )
| A.4 | B.5 | C.6 | D.10 |
数列 前
前 项和为
项和为 ,若
,若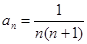 ,则
,则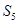 =( )
=( )
A.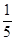 | B.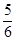 | C.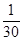 | D.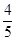 |
已知数列 满足
满足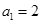 ,
,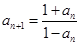 (
( N*),则连乘积
N*),则连乘积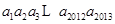 的值为( )
的值为( )
A.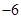 | B.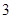 | C.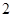 | D.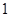 |
数列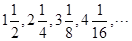 前n项的和为()
前n项的和为()
A.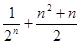 | B.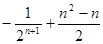 |
C.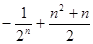 | D.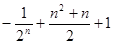 |
 是定义在
是定义在 上恒不为零的函数,对任意实数
上恒不为零的函数,对任意实数 、
、 ,都有
,都有 ,若
,若 ,
, (
( ),则数列
),则数列 的前
的前 项和
项和 的取值范围是 ( )
的取值范围是 ( )



 为n个正数a1+a2+…+an的“均倒数”已知数列{an}的各项均为正,且其前n项的“均倒数”为
为n个正数a1+a2+…+an的“均倒数”已知数列{an}的各项均为正,且其前n项的“均倒数”为 则数列{an}的通项公式为
则数列{an}的通项公式为