题目内容
已知loga2=m,loga3=n,求a2m+n=
12
12
.分析:化对数式为指数式,得到am=2,an=3,然后利用指数式的运算性质求解.
解答:解:由loga2=m,loga3=n,
得:am=2,an=3.
∴a2m+n=(am)2•an=22×3=12.
故答案为:12.
得:am=2,an=3.
∴a2m+n=(am)2•an=22×3=12.
故答案为:12.
点评:本题考查了指数式和对数式的互化,考查了指数式的运算性质,是基础题.

练习册系列答案
相关题目
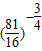 = ,
= ,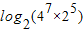 = ;已知loga2=m,loga3=n,a2m+n= .
= ;已知loga2=m,loga3=n,a2m+n= .