题目内容
已知实数a,b∈R+,a+b=1,M=2a+2b,则M的整数部分是( )A.1
B.2
C.3
D.4
【答案】分析:由a,b∈R+,a+b=1,M=2a+2b,可将M=2a+2b,转化为:M=2a+ ,根据a∈(0,1)可求得M的取值范围,从而可求得M的整数部分,继而得到答案.
,根据a∈(0,1)可求得M的取值范围,从而可求得M的整数部分,继而得到答案.
解答:解:∵a,b∈R+,a+b=1,
∴b=1-a,
∴M=2a+2b=,2a+ ,a∈(0,1)
,a∈(0,1)
令t=2a,a∈(0,1),则t∈(1,2),M=t+ ,t∈(1,2).
,t∈(1,2).
∵M=t+ 在(1,
在(1,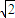 ]上单调递减,在[
]上单调递减,在[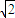 ,2)上单调递增,
,2)上单调递增,
∴Mmin= +
+ =2
=2 ,当t=1或t=2,M=3,
,当t=1或t=2,M=3,
∴2 ≤M<3.
≤M<3.
故选B.
点评:本题考查函数的单调性与最值,难点在于对“双钩函数M=t+ (由于t∈(1,2),在这里是“单钩“)”性质的掌握与应用,属于中档题.
(由于t∈(1,2),在这里是“单钩“)”性质的掌握与应用,属于中档题.
 ,根据a∈(0,1)可求得M的取值范围,从而可求得M的整数部分,继而得到答案.
,根据a∈(0,1)可求得M的取值范围,从而可求得M的整数部分,继而得到答案.解答:解:∵a,b∈R+,a+b=1,
∴b=1-a,
∴M=2a+2b=,2a+
 ,a∈(0,1)
,a∈(0,1)令t=2a,a∈(0,1),则t∈(1,2),M=t+
 ,t∈(1,2).
,t∈(1,2).∵M=t+
 在(1,
在(1,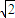 ]上单调递减,在[
]上单调递减,在[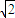 ,2)上单调递增,
,2)上单调递增,∴Mmin=
 +
+ =2
=2 ,当t=1或t=2,M=3,
,当t=1或t=2,M=3,∴2
 ≤M<3.
≤M<3.故选B.
点评:本题考查函数的单调性与最值,难点在于对“双钩函数M=t+
 (由于t∈(1,2),在这里是“单钩“)”性质的掌握与应用,属于中档题.
(由于t∈(1,2),在这里是“单钩“)”性质的掌握与应用,属于中档题. 
练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目