题目内容
(满分12分) 已知函数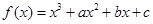 在
在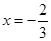 与
与 时都取得极值
时都取得极值
(1)求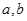 的值与函数
的值与函数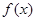 的单调区间
的单调区间
(2)若对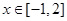 ,不等式
,不等式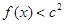 恒成立,求c的取值范围
恒成立,求c的取值范围
【答案】
(1)以函数 的递增区间是
的递增区间是 与
与 ,递减区间是
,递减区间是 ;
;
(2)
【解析】本试题主要是考查了导致在研究函数中的运用,利用极值点处导数为零得到参数的值,进而分析函数的单调性和单调区间的求解的综合运用,以及函数给定闭区间的最值问题。
(1)根据函数在两个点处取得极值,说明导数都为零得到参数a,b的值,进而求解单调区间的问题。
(2)要是不等式恒成立,只要求解函数在给定区间的的最大值即可。
(1)
由 ,
, 得
得
 ,函数
,函数 的单调区间如下表:
的单调区间如下表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
极大值 |
¯ |
极小值 |
|
所以函数 的递增区间是
的递增区间是 与
与 ,递减区间是
,递减区间是 ;
;
(2) ,当
,当 时,
时,
为极大值,而 ,则
,则 为最大值,要使
为最大值,要使
恒成立,则只需要 ,得
,得

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目



 bc.
bc. (常数
(常数 ),P是曲线C上的动点,M是曲线C的右
),P是曲线C上的动点,M是曲线C的右 ,求|PA|的最大值与最小值.
,求|PA|的最大值与最小值. 的取值范围.
的取值范围. ,
,
 时,
时, 在其定义域内单调递增,求
在其定义域内单调递增,求 的取值范围;
的取值范围; 的图象
的图象 与函数
与函数 的图象
的图象 交于
交于 ,
, 两点,过线段
两点,过线段 的中点
的中点 作
作 轴的垂线分别交
轴的垂线分别交 ,
, ,问是否存在点
,问是否存在点