题目内容
(本题满分14分)
如图,酒杯的形状为倒立的圆锥,杯深8 cm .上口宽6cm , 水以20 cm3/s的流量倒入杯中,当水深为4 cm时,求水升高的瞬时变化率.

解法一:设时刻t s时,杯中水的体积为Vcm3,水面半径为r cm, 水深为h cm.
则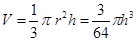 2分
2分
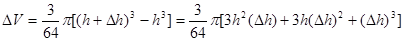 5分
5分
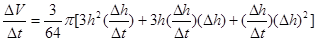 7分
7分
记水升高的瞬时变化率为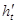 (即当
(即当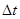 无限趋近于0时,
无限趋近于0时,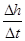 无限趋近于
无限趋近于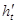 )
)
从而有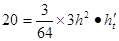 ,当h=4时,解得
,当h=4时,解得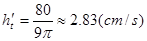 12分
12分
答:当水深为4 cm时,水升高的瞬时变化率为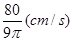 。
14分
。
14分
解法二:仿解法一,可得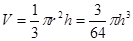 ,即
,即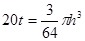 4分
4分
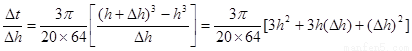 5分
5分
当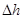 无限趋近于0时,
无限趋近于0时,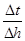 无限趋近于
无限趋近于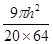 ,即
,即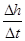 无限趋近于
无限趋近于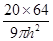 12分
12分
当h=4时,水升高的瞬时变化率是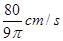 .
14分
.
14分
解法三:水面高为4 cm时,可求得水面半径为 ,设水面高度增加
,设水面高度增加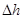 时,水的体积增加
时,水的体积增加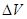 ,从而
,从而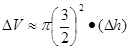 ,(用圆柱近似增加的水体积) ,
8分
,(用圆柱近似增加的水体积) ,
8分
故 .当
.当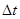 无限趋近于0时得
无限趋近于0时得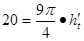 10分
10分
即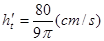 12分
12分
答:当水深为4 cm时,水升高的瞬时变化率为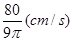 。
14分
。
14分
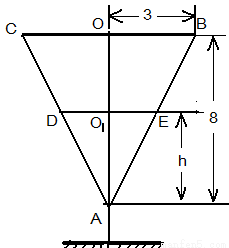
解法四:设t 时刻时注入杯中的水的高度为 h ,杯中水面为圆形,其圆半径为r 1分
如图被子的轴截面为等腰三角形ABC,AO1O为底边BC上的高,O1,O 分别为DE,BC中点,
容易求证 ∽
∽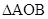 ,那么
,那么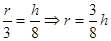 2分
2分
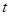 时刻时杯中水的容积为V=
时刻时杯中水的容积为V=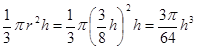 3分
3分
又因为V=20t, 4分
 则
则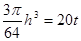 即
即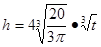 6分
6分
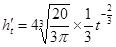 8分
8分
当h=4 时,设t=t1,
由三角形形似的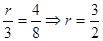 ,
9分
,
9分
那么
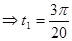 10分
10分
答:当水高为4 cm时,水升高的瞬时变化率为 cm/s
14分
cm/s
14分
【解析】略

 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
 B=[0,3],求实数m的值
B=[0,3],求实数m的值 CRB,求实数m的取值范围
CRB,求实数m的取值范围 是⊙
是⊙ :
: 上的任意一点,过
上的任意一点,过 垂直
垂直 轴于
轴于 ,动点
,动点 满足
满足 。
。 ,在动点
,在动点 、
、 ,使
,使 (O是坐标原点),若存在,求出直线
(O是坐标原点),若存在,求出直线 的方程,若不存在,请说明理由。
的方程,若不存在,请说明理由。 .
. 的定义域;
的定义域; 是否有根?如果有根
是否有根?如果有根 ,请求出一个长度为
,请求出一个长度为 的区间
的区间 ,使
,使
 ).
).