题目内容
如图,在直三棱柱ABC—A1B1C1中,∠ACB=90°,CB=1,CA=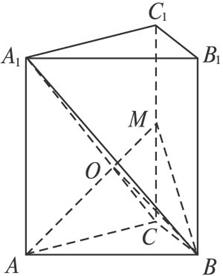
(1)求证:AM⊥平面A1BC;
(2)求二面角B-AM-C的大小;
(3)求点C到平面ABM的距离.
(文)如图,在直三棱柱ABC—A1B1C1中,∠ACB=90°,CB=1,CA=![]() , AA1=
, AA1=![]() ,M为侧棱CC1上一点,AM⊥A1C.
,M为侧棱CC1上一点,AM⊥A1C.
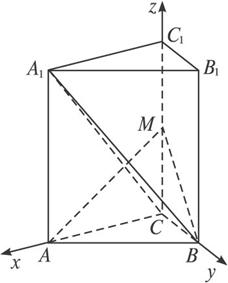
(1)求异面直线A1B与AC所成的角的余弦值;
(2)求证:AM⊥平面A1BC;
(3)求二面角M-AB-C的正切值.
解法一:(1)证明:在直三棱柱ABC—A1B1C1中,易知面ACC1A1⊥面ABC,
∵∠ACB=90°,
∴BC⊥面ACC1A1.
∵AM![]() 面ACC1A1,∴BC⊥AM.
面ACC1A1,∴BC⊥AM.
∵AM⊥BA1,且BC∩BA1=B,
∴AM⊥平面A1BC.

(2)解:设AM与A1C的交点为O,连结BO,
由(1)可知AM⊥OB,且AM⊥OC,
∴∠BOC为二面角B-AM-C的平面角.
在Rt△ACM和Rt△A1AC中,∠OAC+∠ACO=90°,
∴∠AA1C=∠MAC.
∴Rt△ACM∽Rt△A1AC.
∴AC2=MC·AA1.
∴MC=![]() .
.
∴在Rt△ACM中,AM=![]() .
.
∵![]() AC·MC=
AC·MC=![]() AM·CO,
AM·CO,
∴CO=1.
∴在Rt△BCO中,tan∠BOC=![]() =1.
=1.
∴∠BOC=45°,
故所求二面角的大小为45°.
(3)解:设点C到平面ABM的距离为h,易知BO=![]() ,
,
可知S△ABM=![]() ·AM·BO=
·AM·BO=![]() ×
×![]() ×
×![]() =
=![]() .
.
∵VC-ABM=VM-ABC,
∴![]() hS△ABM=
hS△ABM=![]() MC·S△ABC.
MC·S△ABC.
∴h=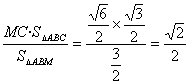 .
.
∴点C到平面ABM的距离为![]() .
.
解法二:(1)同解法一.
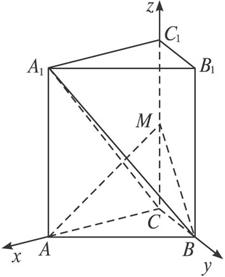
(2)如图以C为原点,CA、CB、CC1所在直线分别为x轴、y轴、z轴,建立空间直角坐标系,

则A(![]() ,0,0),A1(
,0,0),A1(![]() ,0,
,0,![]() ),B(0,1,0),
),B(0,1,0),
设M(0,0,z1),
∵AM⊥BA1,
∴![]() =0,
=0,
即-3+0+![]() z1=0,
z1=0,
故z1=![]() .
.
∴M(0,0,![]() ).
).
设向量m=(x,y,z)为平面AMB的法向量,
则m⊥![]() ,m⊥
,m⊥![]() ,
,
则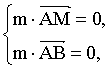
即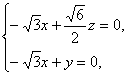
令x=1,平面AMB的一个法向量为m=(1,![]() ,
,![]() ),
),
显然向量![]() 是平面AMC的一个法向量,
是平面AMC的一个法向量,
cos〈m,![]() 〉=
〉=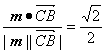 .
.
易知,m与![]() 所夹的角等于二面角B-AM-C的大小,故所求二面角的大小为45°.
所夹的角等于二面角B-AM-C的大小,故所求二面角的大小为45°.
(3)所求距离为![]() ,
,
即点C到平面ABM的距离为![]() .
.
(文)解法一:(1)在直三棱柱ABC—A1B1C1中,
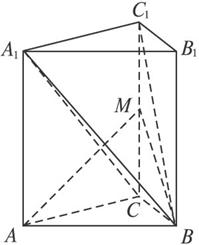
AC∥A1C1,∴∠BA1C1是异面直线A1B与AC所成的角.
连结BC1,
∵CC1⊥平面A1B1C1,
∴CC1⊥A1C1.
又∠A1C1B1=∠ACB=90°,即A1C1⊥B1C1,
∴A1C1⊥平面BB1C1C.
∵BC1![]() 平面BB1C1C,
平面BB1C1C,
∴A1C1⊥BC1.
在Rt△BCC1中,BC=1,CC1=AA1=![]() ,
,
∴BC1=![]() .
.
在Rt△A1BC1中,A1C1=![]() ,BC1=
,BC1=![]() ,
,
∴A1B=![]() .
.
∴cos∠BA1C1=![]() .
.
(2)证明:由(1)可知BC⊥AC,BC⊥CC1,
∴BC⊥平面ACC1A1.
又AM![]() 平面ACC1A1,则BC⊥AM.
平面ACC1A1,则BC⊥AM.
∵AM⊥A1C,
∴AM⊥平面A1BC.
(3)在△ABC中,作AB边上的高CH,垂足为H,连结MH,显然CH是MH在平面ABC上的射影.
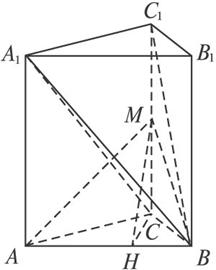
∴MH⊥AB.
∴∠MHC是二面角M-AB-C的平面角.
∵AM⊥A1C,
∴∠MAC=∠AA1C,则tan∠MAC=tan∠AA1C,
即![]() .
.
又AA1=![]() ,AC=
,AC=![]() ,
,
∴MC=![]() .
.
又CH=![]() ,
,
故在Rt△MCH中,
tan∠MHC=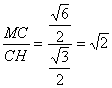 .
.
解法二:(1)如图,以C为原点,CA、CB、CC1所在直线分别为x轴、y轴、z轴,建立空间直角坐标系,则C(0,0,0),A(![]() ,0,0),A1(
,0,0),A1(![]() ,0,
,0,![]() ),B(0,1,0),
),B(0,1,0),
∴![]() =(
=(![]() ,1,
,1,![]() ),
),![]() =(
=(![]() ,0,0).
,0,0).
设异面直线A1B与AC所成的角为θ1,则
cosθ1=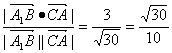 .
.
(2)同解法一.
(3)设M(0,0,z1),
∵AM⊥A1C,∴![]() =0,
=0,
即-3+0+![]() z1=0,故z1=
z1=0,故z1=![]() .
.
∴M(0,0,![]() ).
).
设向量m=(x,y,z)为平面AMB的法向量,
则m⊥![]() ,m⊥
,m⊥![]() ,
,
则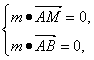
即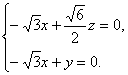 令x=1,
令x=1,
则平面AMB的一个法向量为m=(1,![]() ),
),
显然向量n=(0,0,1)是平面ABC的一个法向量.
设所求二面角的大小为θ2,
则cosθ2=![]() .
.
∴tanθ2=![]() .
.

 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案



