题目内容
设a为实数,函数f(x+a)=(x+a)|x|,x∈R.(1)求f(x)的解析式;
(2)若f(1)>2,求a的取值范围;
(3)当0≤x≤1时,求f(x)的最大值g(a).
分析:(1)用换元法求f(x)的解析式(2)解关于a的绝对值不等式;(3)转化函数为分段函数,每一段用二次函数求得最值,两段中取最大的.
解答: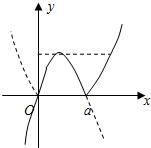 解:(1)令x+a=t,
解:(1)令x+a=t,
∴x=t-a,
∴f(t)=t|t-a|.
∴f(x)=x|x-a|(x∈R).
(2)∵f(1)>2,
∴|1-a|>2,
∴a-1>2或a-1<-2,
∴a>3或a<-1,
∴a的取值范围是a>3或a<-1.
(3)f(x)=
当a≤0时,f(x)在[0,1]单调递增,
∴fmax(x)=f(1)=1-a.
当a>0时,f(x)的图象如图:
①当
>12时,即a>23时,
fmax(x)=f2(1)=a-1.
②由f1(x)=
,x>a得,
∴x2-ax-
=0,
∴x=
.
∵x>a,
∴x=
舍去,
∴x=
.
∴当
≤1≤
时,
即2(
-1)≤a≤2时,fmax(x)=
.
③当
<1时,
即0<a<2(
-1),
fmax(x)=f1(1)=1-a.
综上所述,g(a)=
.
 解:(1)令x+a=t,
解:(1)令x+a=t,∴x=t-a,
∴f(t)=t|t-a|.
∴f(x)=x|x-a|(x∈R).
(2)∵f(1)>2,
∴|1-a|>2,
∴a-1>2或a-1<-2,
∴a>3或a<-1,
∴a的取值范围是a>3或a<-1.
(3)f(x)=
|
当a≤0时,f(x)在[0,1]单调递增,
∴fmax(x)=f(1)=1-a.
当a>0时,f(x)的图象如图:
①当
| a |
| 2 |
fmax(x)=f2(1)=a-1.
②由f1(x)=
| a2 |
| 4 |
∴x2-ax-
| a2 |
| 4 |
∴x=
(1±
| ||
| 2 |
∵x>a,
∴x=
(1-
| ||
| 2 |
∴x=
(1+
| ||
| 2 |
∴当
| a |
| 2 |
(1+
| ||
| 2 |
即2(
| 2 |
| a2 |
| 4 |
③当
(1+
| ||
| 2 |
即0<a<2(
| 2 |
fmax(x)=f1(1)=1-a.
综上所述,g(a)=
|
点评:本题主要考查绝对值函数,分段函数和二次函数与方程不等式的内在联系,特别要注意分类讨论思想的应用.

练习册系列答案
相关题目