Question

已知π＜α+β＜，-π＜α-β＜-，求2α-β的范围.

Answer 1

思路解析：本题若直接由α+β的范围与α-β的范围相加减来求出α、β的范围，则所得α、β的范围都比实际大，从而导致结果错误.此题只能用α+β和α-β表示2α-β，从而得出结果.

解：设2α-β=A(α+β)+B(α-β)(A、B为待定系数)，则

2α-β=(A+B)α+(A-B)β,           ①

比较①式左右两边得：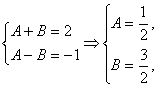

∴2α-β=(α+β)+(α-β).

而＜(α+β)＜，-＜(α-β)＜-，

∴-π＜2α-β＜.