题目内容
(12分)已知直线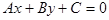 ,
,
(1)系数为什么值时,方程表示通过原点的直线;
(2)系数满足什么关系时与坐标轴都相交;
(3)系数满足什么条件时只与x轴相交;
(4)系数满足什么条件时是x轴;
(5)设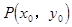 为直线
为直线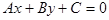 上一点,
上一点,
证明:这条直线的方程可以写成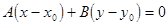 .
.
【答案】
(1)C=0,A、B不同为零.(2)A、B应均不为零.(3)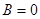 且
且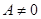 .
.
(4)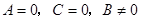 .(5)见解析。
.(5)见解析。
【解析】
试题分析:解:(1)采用“代点法”,将O(0,0)代入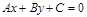 中得C=0,A、B不同为零.
中得C=0,A、B不同为零.
(2)直线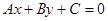 与坐标轴都相交,说明横纵截距
与坐标轴都相交,说明横纵截距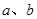 均存在.设
均存在.设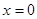 ,得
,得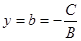 ;设
;设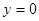 ,得
,得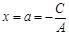 均成立,因此系数A、B应均不为零.
均成立,因此系数A、B应均不为零.
(3)直线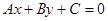 只与x轴相交,就是指与y轴不相交——平行、重合均可。因此直线方程将化成
只与x轴相交,就是指与y轴不相交——平行、重合均可。因此直线方程将化成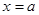 的形式,故
的形式,故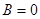 且
且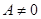 为所求.
为所求.
(4)x轴的方程为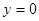 ,直线方程
,直线方程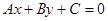 中
中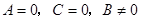 即可.注意B可以不为1,即
即可.注意B可以不为1,即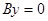 也可以等价转化为
也可以等价转化为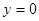 .
.
(5)运用“代点法”.
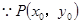 在直线
在直线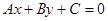 上,
上,
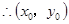 满足方程
满足方程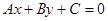 , 即
, 即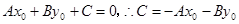 ,
,
故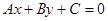 可化为
可化为 ,
,
即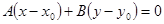 ,得证.
,得证.
考点:本题主要考查直线方程的一般式。
点评:深刻理解直线方程的一般式,明确系数A,B,C的意义及其作用。

练习册系列答案
相关题目
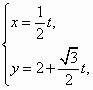 (t为参数),曲线C的极坐标方程为
(t为参数),曲线C的极坐标方程为 (φ为参数),那么直线和椭圆的公共点个数为( )
(φ为参数),那么直线和椭圆的公共点个数为( ) 的外接圆,D是的中点,BD交AC于E。
的外接圆,D是的中点,BD交AC于E。
 O到AC的距离为1,求⊙O的半径。
O到AC的距离为1,求⊙O的半径。 的参数方程为
的参数方程为 (t为参数),曲线C的极坐标方程为
(t为参数),曲线C的极坐标方程为 ,以极点为原点,极轴为x轴正半轴建立直角坐标系,M点坐标为(0,2),直线
,以极点为原点,极轴为x轴正半轴建立直角坐标系,M点坐标为(0,2),直线

 的图象;
的图象; 恒成立,求a-b的最大值。
恒成立,求a-b的最大值。 的外接圆,D是的中点,BD交AC于E。
的外接圆,D是的中点,BD交AC于E。
 O到AC的距离为1,求⊙O的半径。
O到AC的距离为1,求⊙O的半径。 的参数方程为
的参数方程为 (t为参数),曲线C的极坐标方程为
(t为参数),曲线C的极坐标方程为 ,以极点为原点,极轴为x轴正半轴建立直角坐标系,M点坐标为(0,2),直线
,以极点为原点,极轴为x轴正半轴建立直角坐标系,M点坐标为(0,2),直线

 的图象;
的图象; 恒成立,求a-b的最大值。
恒成立,求a-b的最大值。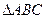 的外接圆,D是的中点,BD交AC于E。
的外接圆,D是的中点,BD交AC于E。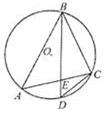
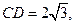 O到AC的距离为1,求⊙O的半径。
O到AC的距离为1,求⊙O的半径。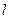 的参数方程为
的参数方程为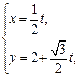 (t为参数),曲线C的极坐标方程为
(t为参数),曲线C的极坐标方程为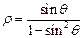 ,以极点为原点,极轴为x轴正半轴建立直角坐标系,M点坐标为(0,2),直线
,以极点为原点,极轴为x轴正半轴建立直角坐标系,M点坐标为(0,2),直线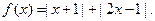
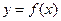 的图象;
的图象; 恒成立,求a-b的最大值。
恒成立,求a-b的最大值。