题目内容
.设正项数列 的前
的前 项和为
项和为 ,满足
,满足 ,
, .
.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)设 ,证明:
,证明:
【答案】
解:(I) ,
,

 ,
,
两式相减得: ,
, ………… 2分
………… 2分
得
由于 ,所以
,所以 ,从而有
,从而有  ,
, ………… 4分
………… 4分
又由 ,且
,且 得
得
所以 是以2为首项,2为公差的等差数列,
是以2为首项,2为公差的等差数列, ,
, ………… 6分
………… 6分
(II)由(I)得
 … 8分
… 8分
 时,
时,

 (
( 时取等号)
………… 10分
时取等号)
………… 10分
又
故 ………… 12分
………… 12分

练习册系列答案
 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案
相关题目
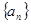 的前
的前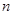 项和是
项和是 ,若
,若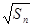 }都是等差数列,且公差相等,则
}都是等差数列,且公差相等,则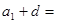
 的前
的前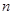 项和为
项和为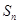 ,满足
,满足 ,
, .(Ⅰ)求数列
.(Ⅰ)求数列 ,证明:
,证明: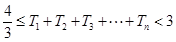
 }的前
}的前 项和
项和 ,对于任意
,对于任意 点
点 都在函数
都在函数 的图象上.
的图象上.  的前n项和为
的前n项和为 ,求
,求