题目内容
6.已知α,β∈(0,$\frac{π}{2}$),且cosα=$\frac{5}{13}$,sin(α-β)=$\frac{4}{5}$,则sinβ=$\frac{16}{65}$.分析 由已知可求范围α-β∈(-$\frac{π}{2}$,$\frac{π}{2}$),由同角三角函数基本关系式可求sinα,cos(α-β)的值,利用角的关系式β=(β-α)+α及两角和的正弦函数公式即可计算求值.
解答 解:∵α,β∈(0,$\frac{π}{2}$),且cosα=$\frac{5}{13}$,sin(α-β)=$\frac{4}{5}$,
∴α-β∈(-$\frac{π}{2}$,$\frac{π}{2}$),sinα=$\sqrt{1-co{s}^{2}α}$=$\frac{12}{13}$,cos(α-β)=$\sqrt{1-si{n}^{2}(α-β)}$=$\frac{3}{5}$,
∴sinβ=sin[(β-α)+α]=sin(β-α)cosα+cos(β-α)sinα=-sin(α-β)cosα+cos(α-β)sinα=(-$\frac{4}{5}$)×$\frac{5}{13}$+$\frac{3}{5}×\frac{12}{13}$=$\frac{16}{65}$.
故答案为:$\frac{16}{65}$.
点评 本题主要考查了同角三角函数基本关系式,两角和的正弦函数公式,诱导公式在三角函数化简求值中的应用,考查了计算能力和转化思想,属于基础题.

练习册系列答案
相关题目
16.已知直线l过抛物线E:y2=4x的焦点F,且依次交抛物线E及其准线于点A,B,C(点B在点A,C之间)若|BC|=2|BF|,则|AF|=( )
| A. | $\frac{4}{3}$ | B. | 4 | C. | 6 | D. | 12 |
17.已知复数z满足z=1+i(2+i)(i为虚数单位),则|z|等于( )
| A. | 2 | B. | 2$\sqrt{2}$ | C. | 4 | D. | 8 |
14.sin810°+cos(-60°)=( )
| A. | $\frac{3}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{2-\sqrt{3}}{2}$ |
1.已知sin($\frac{π}{5}$-θ)=$\frac{\sqrt{6}}{3}$,那么sin($\frac{11π}{10}$+2θ)=( )
| A. | $\frac{1}{3}$ | B. | -$\frac{\sqrt{6}}{3}$ | C. | $\frac{2\sqrt{2}}{3}$ | D. | -$\frac{\sqrt{3}}{3}$ |
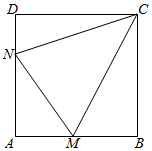 如图所示,某村积极开展“美丽乡村•生态家园”建设,现拟在边长为1千米的正方形地块ABCD上划出一片三角形地块CMN建设美丽乡村生态公园,给村民休闲健身提供去处.点M,N分别在边AB,AD上.
如图所示,某村积极开展“美丽乡村•生态家园”建设,现拟在边长为1千米的正方形地块ABCD上划出一片三角形地块CMN建设美丽乡村生态公园,给村民休闲健身提供去处.点M,N分别在边AB,AD上.