题目内容
设![]() ,
,![]() .令
.令![]() ,讨论
,讨论![]() 在
在![]() 内的单调性并求极值;
内的单调性并求极值;
知![]() 在
在![]() 内是减函数,在
内是减函数,在![]() 内是增函数,
内是增函数, ![]() 处取得极小值
处取得极小值![]() .
.
解析:
根据求导法则有![]() ,
,
故![]() ,于是
,于是![]() ,
,
|
|
| 2 |
|
|
|
|
|
|
|
| 减 | 极小值 | 增 |
列表如下:
故知![]() 在
在![]() 内是减函数,在
内是减函数,在![]() 内是增函数,所以,在
内是增函数,所以,在![]() 处取得极小值
处取得极小值![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
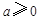 ,
,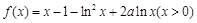 .
.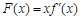 ,讨论
,讨论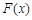 在
在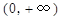 内的单调性并求极值;
内的单调性并求极值; 时,试判断
时,试判断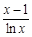 与
与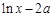 的大小.
的大小. ,
, .
. ,讨论
,讨论 在
在 内的单调性并求极值;
内的单调性并求极值; 时,恒有
时,恒有 .
. ,
, .
. ,讨论
,讨论 在
在 内的单调性并求极值;
内的单调性并求极值; 时,恒有
时,恒有 .
.