题目内容
设 ,
, .
.
(Ⅰ)令 ,讨论
,讨论 在
在 内的单调性并求极值;
内的单调性并求极值;
(Ⅱ)求证:当 时,恒有
时,恒有 .
.
【答案】
本小题主要考查函数导数的概念与计算,利用导数研究函数的单调性、极值和证明不等式的方法,考查综合运用有关知识解决问题的能力.本小题满分14分。
(Ⅰ)解:根据求导法则有 ,
,
故 ,
,
于是 ,
,
列表如下:
|
|
|
2 |
|
|
|
|
0 |
|
|
|
|
极小值 |
|
故知 在
在 内是减函数,在
内是减函数,在 内是增函数,所以,在
内是增函数,所以,在 处取得极小值
处取得极小值 。
。
(Ⅱ)证明:由 知,
知, 的极小值
的极小值 。
。
于是由上表知,对一切 ,恒有
,恒有 。
。
从而当 时,恒有
时,恒有 ,故
,故 在
在 内单调增加。
内单调增加。
所以当 时,
时, ,即
,即 。
。
故当 时,恒有
时,恒有 。
。

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目






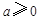 ,
,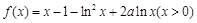 .
.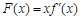 ,讨论
,讨论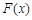 在
在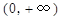 内的单调性并求极值;
内的单调性并求极值; 时,试判断
时,试判断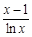 与
与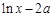 的大小.
的大小. ,
, .
. ,讨论
,讨论 在
在 内的单调性并求极值;
内的单调性并求极值; 时,恒有
时,恒有 .
.