题目内容
4．若函数f（x）=$\left\{\begin{array}{l}{{x}^{2}，x＞0}\\{π，x=0}\\{0，x＜0}\end{array}\right.$，则f{f[f（-2）]}=（ ）| A． | 0 | B． | π | C． | π2 | D． | 4 |
分析 直接利用分段函数求解函数值即可．
解答 解：函数f（x）=$\left\{\begin{array}{l}{{x}^{2}，x＞0}\\{π，x=0}\\{0，x＜0}\end{array}\right.$，
则f（-2）=0，
f（f（-2））=f（0）=π．
f{f[f（-2）]}=f（π）=π2．
故选：C．
点评 本题考查分段函数的应用，函数值的求法，考查计算能力．
练习册系列答案
阶梯计算系列答案
相关题目
14．若tan（θ+$\frac{π}{4}$）=-3，则$\frac{sin2θ}{1+cos2θ}$=（ ）
| A． | -1 | B． | 1 | C． | -2 | D． | 2 |
15．执行下面的程序框图，若p=0.95，则输出的n=（ ）
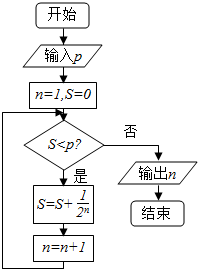
| A． | 4 | B． | 5 | C． | 6 | D． | 7 |
19．数据5，7，7，8，10，11的方差是（ ）
| A． | 24 | B． | 10 | C． | 4 | D． | 2 |
9．函数f（x）=lg（2x-3）的定义域是（ ）
| A． | [$\frac{3}{2}$，+∞） | B． | （$\frac{3}{2}$，+∞） | C． | （-∞，$\frac{3}{2}$] | D． | （-∞，$\frac{3}{2}$） |