Question

如图,四边形ABCD为平行四边形，四边形ADEF是正方形，且BD⊥平面CDE，H是BE的中点,G是AE,DF的交点.

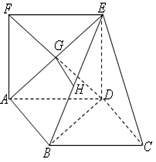
（1）求证:GH∥平面CDE；

（2）求证:面ADEF⊥面ABCD.

 

Answer 1

【答案】

（1）见解析；（2）见解析.

【解析】

试题分析：（1）先利用三角形中位线知识证，再利用ABCD为平行四边形证AB∥CD，进而证明平面；（2）由得，再证明即可.

试题解析：⑴是的交点，∴是中点，又是的中点，

∴中，，                             2分

∵ABCD为平行四边形

∴AB∥CD

∴，                                                  4分

又∵

∴平面                                       7分

⑵，

所以，                                          9分

又因为四边形为正方形，

，                                            10分

，

，                                        12分

 

.                                   14分

考点：空间中直线和平面、平面和平面间的位置关系.