题目内容
已知曲线![]() :
:![]() ,数列
,数列![]() 的首项
的首项![]() ,且当
,且当![]() 时,点
时,点![]() 恒在曲线
恒在曲线![]() 上,数列
上,数列![]() 满足
满足![]() .
.
(1)试判断数列![]() 是否是等差数列?并说明理由;
是否是等差数列?并说明理由;
(2)求数列![]() 和
和![]() 的通项公式;
的通项公式;
(3)设数列![]() 满足
满足![]() ,试比较数列
,试比较数列![]() 的前n项和
的前n项和![]() 与2的大小.
与2的大小.
(1)数列![]() 是公差为
是公差为![]() 的等差数列.
的等差数列.
(2)![]() ;
; ![]()
(3)![]()
![]()
解析:
(1)∵当![]() 时,点
时,点![]() 恒在曲线
恒在曲线![]() 上
上
∴![]() -----------------------------------------------1分
-----------------------------------------------1分
由![]() 得
得
当![]() 时,
时,![]()
![]()
![]()
![]() ----5分
----5分
∴数列![]() 是公差为
是公差为![]() 的等差数列.-------------------------------------------------------6分
的等差数列.-------------------------------------------------------6分
(2)∵![]() =4,∴
=4,∴![]()
∴![]() -----------------------------------8分
-----------------------------------8分
由![]() 得
得![]() -----------------------------------------------10分
-----------------------------------------------10分
(3)∵![]() ∴
∴![]() =
=![]() ----------------------12分
----------------------12分
∴![]()
![]()
![]() -----14分
-----14分

练习册系列答案
相关题目
 :
: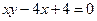 ,数列
,数列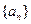 的首项
的首项 ,且当
,且当 时,点
时,点 恒在曲线
恒在曲线 满足
满足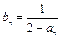 .
.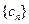 满足
满足 ,试比较数列
,试比较数列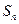 与2的大小.
与2的大小.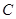 :
: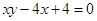 ,数列
,数列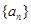 的首项
的首项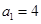 ,且当
,且当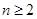 时,点
时,点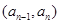 恒在曲线
恒在曲线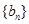 满足
满足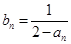 。
。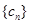 满足
满足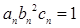 ,试比较数列
,试比较数列 项和
项和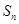 与2的大小。
与2的大小。