题目内容
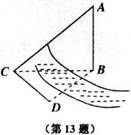
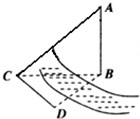 如图,测量河对岸的旗杆高AB时,选与旗杆底B在同一水平面内的两个测点C与D,测得∠BCD=75°,∠BDC=60°,CD=a,并在点C测得旗杆顶A的仰角为60°,则旗杆高AB为
如图,测量河对岸的旗杆高AB时,选与旗杆底B在同一水平面内的两个测点C与D,测得∠BCD=75°,∠BDC=60°,CD=a,并在点C测得旗杆顶A的仰角为60°,则旗杆高AB为3
| ||
| 2 |
3
| ||
| 2 |
分析:在△CBD中根据三角形的内角和定理,求出∠CBD=180°-∠BCD-∠BDC=45°,从而利用正弦定理求出BC.然后在Rt△ABC中,根据三角函数的定义加以计算,可得旗杆AB的高度.
解答:解:∵△BCD中,∠BCD=75°,∠BDC=60°,
∴∠CBD=180°-∠BCD-∠BDC=45°,
在△CBD中,CD=a,根据正弦定理
=
,
可得BC=
=
=
a,
∵Rt△ABC中,∠ACB=60°,
∴AB=BC•tan∠ACB=
a•tan60°=
a,即旗杆高为
a.
故答案为:
a
∴∠CBD=180°-∠BCD-∠BDC=45°,
在△CBD中,CD=a,根据正弦定理
| BC |
| sin∠BDC |
| CD |
| sin∠CBD |
可得BC=
| CD•sin∠BDC |
| sin∠CBD |
| a•sin60° |
| sin45° |
| ||
| 2 |
∵Rt△ABC中,∠ACB=60°,
∴AB=BC•tan∠ACB=
| ||
| 2 |
3
| ||
| 2 |
3
| ||
| 2 |
故答案为:
3
| ||
| 2 |
点评:本题给出实际应用问题,求棋杆AB的高度.着重考查了三角形内角和定理、利用正弦定理解三角形和三角函数的定义等知识,属于中档题.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
 如图,测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个侧点C与D.现测得∠BCD=α,∠BDC=β,CD=s,并在点C测得塔顶A的仰角为θ,则塔高AB=
如图,测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个侧点C与D.现测得∠BCD=α,∠BDC=β,CD=s,并在点C测得塔顶A的仰角为θ,则塔高AB=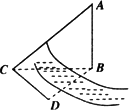
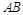 时,选与旗杆底
时,选与旗杆底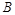 在同一水平面内的两个点
在同一水平面内的两个点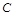 与
与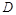 ,测得
,测得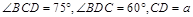 ,并在点
,并在点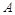 的仰角为
的仰角为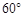 ,则旗杆高
,则旗杆高
 如图,测量河对岸的旗杆高
如图,测量河对岸的旗杆高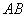 时,选与旗杆底
时,选与旗杆底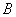 在
在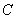 与
与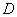 ,测得
,测得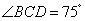 ,
,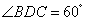 ,
, ,并在点
,并在点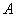 的
的