题目内容
(12分)如图,已知椭圆 的右顶点为A(2,0),点P(2e,
的右顶点为A(2,0),点P(2e, )在椭圆上(e为椭圆的离心率).
)在椭圆上(e为椭圆的离心率).

(1)求椭圆的方程;
(2)若点B,C(C在第一象限)都在椭圆上,满足 ,且
,且 ,求实数λ的值.
,求实数λ的值.
(1) ;(2)
;(2) .
.
【解析】
试题分析:(1)因为椭圆的右顶点为A(2,0),所以 ,又因为点点P(2e,
,又因为点点P(2e, )在椭圆上,所以有
)在椭圆上,所以有 由此解得
由此解得 的值从而得到椭圆的标准方程.
的值从而得到椭圆的标准方程.
(2)设直线的斜率为 ,则直线OC方程为
,则直线OC方程为 ,直线AB方程为
,直线AB方程为 ,分别代入椭圆方程
,分别代入椭圆方程 ,由
,由 ,求出
,求出 ,再由
,再由 ,求出实数
,求出实数 的值.
的值.
试题解析:【解析】
(1)∵椭圆 的右顶点为A(2,0),∴a=2,
的右顶点为A(2,0),∴a=2,
∵点P(2e, )在椭圆上,
)在椭圆上,
∴ ,
,
∵a2=4, ,a2=b2+c2,
,a2=b2+c2,
∴b2=1,c2=3,
∴椭圆的方程为 .
.
(2)设直线OC的斜率为k,则直线OC方程为y=kx,
代入椭圆方程 ,即x2+4y2=4,
,即x2+4y2=4,
得(1+4k2)x2=4,∴ ,
,
∴C( ,
, ),
),
又直线AB方程为y=k(x﹣2),代入椭圆方程x2+4y2=4,
得(1+4k2)x2﹣16k2x+16k2﹣4=0,
∵xA=2,∴xB= ,
,
∵ =0,
=0,
∴ +
+ =0,
=0,
∴ ,∵C在第一象限,∴k>0,∴k=
,∵C在第一象限,∴k>0,∴k= ,
,
∵ =(
=( ),
),
 =(2﹣
=(2﹣ ,0﹣
,0﹣ )=(
)=( ,
, ),
),
由 =
= ,得
,得 ,
,
∴k= ,∴
,∴ .
.
考点:1、椭圆的标准方程;2、直线与椭圆位置关系综合问题.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
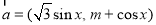 ,
,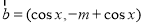 , 且
, 且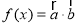 .
.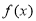 的周期;
的周期;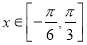 时,
时, 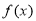 的最小值是-4 , 求此时函数
的最小值是-4 , 求此时函数 的最大值, 及相应的
的最大值, 及相应的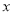 的值.
的值. ,
, ,则
,则 ( )
( ) B.
B. C.
C. D.
D.
 (
( )的一条对称轴是
)的一条对称轴是 ,则函数
,则函数 的最小正周期不可能是( )
的最小正周期不可能是( ) B.
B. C.
C. D.
D.
 ,
, ,则
,则 ( )
( ) B.
B. C.
C. D.
D.
 ,则z=x+2y的最大值为 _________ .
,则z=x+2y的最大值为 _________ .

 时,那么t的取值范围是 _________ .
时,那么t的取值范围是 _________ . 是两个单位向量,它们的夹角是
是两个单位向量,它们的夹角是 ,则
,则
 ;
; ,若函数
,若函数 有3个零点,则0<
有3个零点,则0< <1;
<1; 的定义域和值域都是
的定义域和值域都是 ,则
,则 =1;
=1; 满足
满足 ,则
,则 .
.