题目内容
已知二次函数![]() 对
对![]() 都满足
都满足![]() 且
且![]() ,设函数
,设函数
![]() (
(![]() ,
,![]() ).
).
(Ⅰ)求![]() 的表达式;
的表达式;
(Ⅱ)若![]() ,使
,使![]() 成立,求实数
成立,求实数![]() 的取值范围;
的取值范围;
(Ⅲ)设![]() ,
,![]() ,求证:对于
,求证:对于![]() ,恒有
,恒有![]() .
.
解:(Ⅰ)设![]() ,于是
,于是
![]() 所以
所以
又![]() ,则
,则![]() .所以
.所以![]() . …………3分
. …………3分
(Ⅱ)![]()
当m>0时,由对数函数性质,f(x)的值域为R;…………4分
当m=0时,![]() 对
对![]() ,
,![]() 恒成立; …………5分
恒成立; …………5分
当m<0时,由![]() ,列表:
,列表:
| x |
|
|
|
|
| - | 0 | + |
|
| 减 | 极小 | 增 |
![]()

所以若![]() ,
,![]() 恒成立,则实数m的取值范围是
恒成立,则实数m的取值范围是![]() .
.
故![]() 使
使![]() 成立,实数m的取值范围
成立,实数m的取值范围![]() .…………9分
.…………9分
(Ⅲ)因为对![]() ,
,![]() 所以
所以![]() 在
在![]() 内单调递减.
内单调递减.
于是![]()
![]()
记![]() ,则
,则![]()
所以函数![]() 在
在![]() 是单调增函数,
是单调增函数,
所以![]() ,故命题成立. …………12分
,故命题成立. …………12分

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 对
对 都满足
都满足 且
且 ,设函数
,设函数
 ,
, ).
). ,使
,使 成立,求实数
成立,求实数 的取值范围;
的取值范围;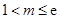 ,
, ,求证:对于
,求证:对于 ,恒有
,恒有 .
. 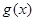 对
对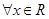 都满足
都满足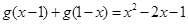 且
且 ,设函数
,设函数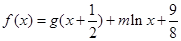 (
(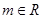 ,
,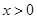 ).
). ,使
,使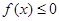 成立,求实数
成立,求实数 的取值范围;
的取值范围; 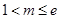 ,
,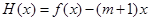 ,求证:对于
,求证:对于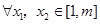 ,恒有
,恒有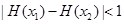 .
.