Question

设函数f（x）=（2x+1）ln（2x+1）．
（Ⅰ）求函数f （x）在点（0，f （0））处的切线方程；
（Ⅱ）求f （x）的极小值；
（Ⅲ）若对所有的x≥0，都有f（x）≥2ax成立，求实数a的取值范围．

Answer 1

分析：（I）欲求在点（0，f（0））处的切线方程，只须求出其斜率的值即可，故先利用导数求出在x=0处的导函数值，再结合导数的几何意义即可求出切线的斜率．从而问题解决．
（II）求出函数的导数，令导数大于0解出其增区间，令导数小于0解出其减区间，并列出如图的x变化时，f'（x），f（x）变化情况进行判断极值即可．
（Ⅲ）令g（x）=（2x+1）ln（2x+1）-2ax，则g'（x）=2ln（2x+1）+2-2a=2[ln（2x+1）+1-a]．令g'（x）=0，得ln（2x+1）=a-1，下面对a进行分类讨论：（1）当a≤1时，（2）当a＞1时，从而求得实数a的取值范围．

解答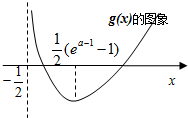：解：（Ⅰ）∵f（x）的定义域为{x|x＞-

1

2

}，又∵f'（x）=2ln（2x+1）+2，
∴k_切线=f'（0）=2，切点为O（0，0），∴所求切线方程为y=2x．…（2分）
（Ⅱ） 设f'（x）=0，得ln（2x+1）=-1，得x=

1

2

(

1

e

-1)；f'（x）＞0，得ln（2x+1）＞-1，得x＞

1

2

(

1

e

-1)；f'（x）＜0，得ln（2x+1）＜-1，得-

1

2

＜x＜

1

2

(

1

e

-1)；
则f(x)极小值=f[

1

2

(

1

e

-1)]=[(

1

e

-1)+1]•ln[(

1

e

-1)+1]=-

1

e

．…（6分）
（Ⅲ）令g（x）=（2x+1）ln（2x+1）-2ax，
则g'（x）=2ln（2x+1）+2-2a=2[ln（2x+1）+1-a]．
令g'（x）=0，得ln（2x+1）=a-1，得x=

1

2

(ea-1-1)；g'（x）＞0，得ln（2x+1）＞a-1，得x＞

1

2

(ea-1-1)；g'（x）＜0，得ln（2x+1）＜a-1，得-

1

2

＜x＜

1

2

(ea-1-1)；
（1）当a≤1时，a-1≤0，∵ea-1≤e0=1⇒ea-1-1≤0⇒

1

2

(ea-1-1)≤0，
∴对所有x≥0时，都有x≥

1

2

(ea-1-1)，于是g'（x）≥0恒成立，
∴g（x）在[0，+∞）上是增函数．
又g（0）=0，于是对所有x≥0，都有g（x）≥g（0）=0成立．
故当a≤1时，对所有的x≥0，都有f（x）≥2ax成立．
（2）当a＞1时，a-1＞0，∵ea-1＞e0=1⇒ea-1-1＞0⇒

1

2

(ea-1-1)＞0，
∴对所有0≤x＜

1

2

(ea-1-1)，都有g'（x）＜0恒成立，
∴g（x）在[0，

1

2

(ea-1-1))上是减函数．
又g（0）=0，于是对所有0≤x＜

1

2

(ea-1-1)，都有g（x）≤g（0）=0．
故当a＞1时，只有对仅有的0≤x＜

1

2

(ea-1-1)，都有f（x）＜2ax．
即当a＞1时，不是对所有的x≥0，都有f（x）≥2ax．
综合（1），（2）可知实数a的取值范围（-∞，1]．…（12分）

点评：本小题主要考查直线的斜率、导数的几何意义、利用导数研究曲线上某点切线方程\利用导数求闭区间上函数的最值，求解的关键是利用导数研究清楚函数的单调性以及根据最值的判断方法确定出函数的最值，此题规律性强．