Question

已知f（x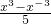）=，g（x）=．
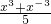（1）求证：f（x）是奇函数，并求f（x）的单调区间；
（2）分别计算f（4）-5f（2）g（2）和f（9）-5f（3）g（3）的值，由此概括出涉及函数f（x）和g（x）对所有不等于零的实数x都成立的一个等式，并加以证明．

Answer 1

解：

（1）函数f（x）的定义域是{x|x≠0}，
∵f（-x）=，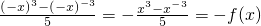
∴f（x）是奇函数．…
设0＜x₁＜x₂，=，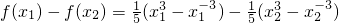
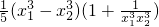∵y=x^3r上是增函数，故，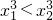
∴f（x₁）-f（x₂）＜0，
即f（x₁）＜f（x₂），∴f（x）在（0，+∞）上是增函数．
又∵f（x）是奇函数，∴f（x）在（-∞，0）上也是增函数．
∴函数f（x）的增区间是（-∞，0）和（0，+∞）．
（2）

=，．
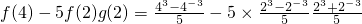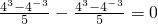同理f（9）-5f（3）g（3）=0．猜想：f（x²）-5f（x）g（x）=0 
证明：

∵．
∴等式成立．

分析：（1）利用函数的奇偶性的定义证明，利用单调性的定义确定函数的单调区间．
（2）分别求出f（4）-5f（2）g（2）和f（9）-5f（3）g（3）的值，然后根据规律得到结论．
点评：本题主要考查函数奇偶性和单调性的判断，综合性较强．