题目内容
设椭圆 恒过定点A(1,2),则椭圆的中心到准线的距离的最小值________.
恒过定点A(1,2),则椭圆的中心到准线的距离的最小值________.
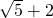
分析:根据椭圆
 恒过定点A(1,2),可得
恒过定点A(1,2),可得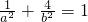 ,利用椭圆几何量之间的关系,设
,利用椭圆几何量之间的关系,设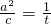 ,等式可转化为t2a4-(t2+1)a2+5=0,利用判别式,即可求得椭圆的中心到准线的距离的最小值.
,等式可转化为t2a4-(t2+1)a2+5=0,利用判别式,即可求得椭圆的中心到准线的距离的最小值.解答:设椭圆的焦距为2c,同时可设
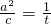 ,∴c=ta2
,∴c=ta2∵椭圆
 恒过定点A(1,2),
恒过定点A(1,2),∴
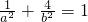
∴b2+4a2=a2b2
∴5a2-c2=a2(a2-c2)
∴5a2-(ta2)2=a2[a2-(ta2)2]
∴t2a4-(t2+1)a2+5=0
∴△=(t2+1)2-20t2≥0时,方程有解
∴
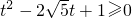
∴t≥
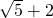 ,或
,或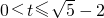
∴
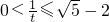 ,或
,或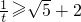
∵椭圆
 恒过定点A(1,2),
恒过定点A(1,2),∴椭圆的中心到准线x=
 >1
>1∴椭圆的中心到准线的距离的最小值
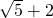
故答案为:
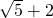
点评:本题综合考查椭圆的标准方程与性质,考查解不等式,考查学生分析解决问题的能力,有一定的技巧.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案
相关题目