题目内容
已知a、b是异面直线,平面M过a且平行于b,平面N过b且平行于a,求证:平面M∥平面N.
思路分析:欲证面面平行,需证线面平行,即在一个平面内找到两条相交直线平行于另一个平面.
证明:如图2-2-11,过a作平面使它交平面N于a′,
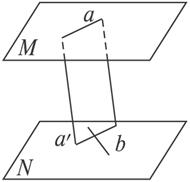
图2-2-11
∵a∥N,
∴a∥a′.
又a
平面M,a′
M,
∴a′∥平面M.
∵a和b是异面直线,
∴a′和b相交.
由a′∥平面M,b∥平面M,得平面M∥平面N.
绿色通道:要证面面平行,只要证线面平行,而要证线面平行,只要证线线平行.在立体几何中,往往通过线线、线面、面面间的位置关系的转化使问题得到解决.
练习册系列答案
阅读快车系列答案
相关题目
