题目内容
已知向量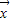 =(
=(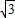 ,-1),
,-1),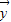 =(
=( ,
,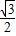 ),若存在实数k和t,使得
),若存在实数k和t,使得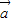 =
=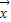 +(t2-3)
+(t2-3)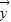 ,
,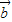 =-k
=-k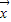 +t
+t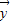 ,且
,且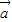 ⊥
⊥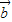 .
.(1)试求函数关系式k=f(t);
(2)若t>0,且不等式f(t)>mt2-t恒成立,求实数m的取值范围.
【答案】分析:(1)根据向量数量积运算公式和模的,算出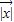 =2,
=2,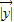 =1且
=1且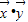 =0,由此化简
=0,由此化简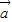 •
•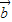 =0的式子得4k+t(t2-3)=0,可得k=f(t)=
=0的式子得4k+t(t2-3)=0,可得k=f(t)= (t3-3t),即为所求函数关系式;
(t3-3t),即为所求函数关系式;
(2)由(1),化简得不等式f(t)>mt2-t恒成立,即m< (t+
(t+ )在(0,+∞)上恒成立.结合基本不等式加以计算,可得m<
)在(0,+∞)上恒成立.结合基本不等式加以计算,可得m< 恒成立,即得实数m的取值范围.
恒成立,即得实数m的取值范围.
解答:解:(1)∵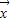 =(
=(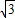 ,-1),
,-1),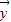 =(
=( ,
,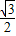 ),
),
∴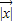 =
=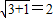 ,
,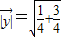 =1,
=1,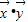 =0
=0
∵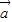 =
=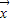 +(t2-3)
+(t2-3)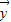 ,
,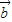 =-k
=-k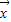 +t
+t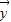 ,且
,且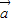 ⊥
⊥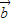 .
.
∴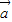 •
•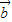 =-k
=-k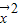 +t(t2-3)
+t(t2-3)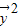 =0,即4k+t(t2-3)=0,
=0,即4k+t(t2-3)=0,
∴t3-3t-4k=0,
可得k=f(t)= (t3-3t),即为所求函数关系式;
(t3-3t),即为所求函数关系式;
(2)不等式f(t)>mt2-t恒成立,
即 (t3-3t)>mt2-t在(0,+∞)上恒成立
(t3-3t)>mt2-t在(0,+∞)上恒成立
化简整理,得m< (t+
(t+ )在(0,+∞)上恒成立
)在(0,+∞)上恒成立
∵t+
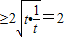 ,当且仅当t=1时,t+
,当且仅当t=1时,t+ 达到最小值2
达到最小值2
∴m< ×2=
×2= ,
,
即满足对任意的t>0,不等式f(t)>mt2-t恒成立的m的取值范围为(-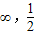 )
)
点评:本题给出向量的坐标,在向量互相垂直的情况下求函数的关系式并参数m的取值范围.着重考查了向量数量积的运算公式、向量的模和不等式恒成立等知识,属于中档题.
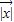 =2,
=2,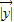 =1且
=1且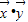 =0,由此化简
=0,由此化简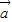 •
•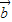 =0的式子得4k+t(t2-3)=0,可得k=f(t)=
=0的式子得4k+t(t2-3)=0,可得k=f(t)= (t3-3t),即为所求函数关系式;
(t3-3t),即为所求函数关系式;(2)由(1),化简得不等式f(t)>mt2-t恒成立,即m<
 (t+
(t+ )在(0,+∞)上恒成立.结合基本不等式加以计算,可得m<
)在(0,+∞)上恒成立.结合基本不等式加以计算,可得m< 恒成立,即得实数m的取值范围.
恒成立,即得实数m的取值范围.解答:解:(1)∵
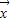 =(
=(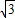 ,-1),
,-1),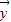 =(
=( ,
,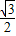 ),
),∴
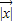 =
=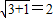 ,
,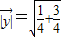 =1,
=1,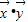 =0
=0 ∵
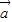 =
=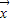 +(t2-3)
+(t2-3)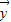 ,
,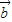 =-k
=-k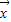 +t
+t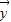 ,且
,且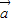 ⊥
⊥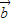 .
.∴
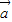 •
•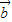 =-k
=-k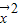 +t(t2-3)
+t(t2-3)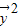 =0,即4k+t(t2-3)=0,
=0,即4k+t(t2-3)=0,∴t3-3t-4k=0,
可得k=f(t)=
 (t3-3t),即为所求函数关系式;
(t3-3t),即为所求函数关系式;(2)不等式f(t)>mt2-t恒成立,
即
 (t3-3t)>mt2-t在(0,+∞)上恒成立
(t3-3t)>mt2-t在(0,+∞)上恒成立化简整理,得m<
 (t+
(t+ )在(0,+∞)上恒成立
)在(0,+∞)上恒成立∵t+

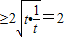 ,当且仅当t=1时,t+
,当且仅当t=1时,t+ 达到最小值2
达到最小值2∴m<
 ×2=
×2= ,
,即满足对任意的t>0,不等式f(t)>mt2-t恒成立的m的取值范围为(-
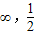 )
)点评:本题给出向量的坐标,在向量互相垂直的情况下求函数的关系式并参数m的取值范围.着重考查了向量数量积的运算公式、向量的模和不等式恒成立等知识,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目