Question

 

已知函数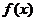=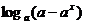（a＞1） ．

   （1）求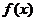的定义域、值域，并判断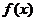的单调性；

   （2）解不等式＞．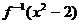

 

 

 

 

 

 

 

 

 

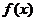Answer 1

【答案】

 

解：（1）为使函数有意义,需满足a－a^x＞0,即a^x＜a,又a＞1,∴x＜1．

故函数定义域为（－∞,1） ．

又由＜=1∴f（x）＜1．即函数的值域为（－∞,1） ．

设x₁＜x₂＜1,则f（x₁）－f（x₂）=－=＞

=0,即f（x₁）＞f（x₂） ．  ∴f（x）为减函数．          …………………6分

（2）设y=,则a^y=a－a^x, ∴a^x=a－a^y,∴x=．

∴f（x）=的反函数为=．

由＞f（x）,得,

∴   解得－1＜x＜1．

故所求不等式的解为－1＜x＜1．                     ……………………12分