题目内容
在三棱锥M-ABC中,CM⊥平面ABC,MA=MB,NA=NB=NC.
(Ⅰ)求证:AM⊥BC;
(Ⅱ)若∠AMB=60°,求直线AM与CN所成的角.
(Ⅰ)求证:AM⊥BC;
(Ⅱ)若∠AMB=60°,求直线AM与CN所成的角.


证明:(I)∵NA=NB=NC,
∴N是△ABC外接圆的圆心,可得∠ACB=90°,即BC⊥AC…(2分)
∵CM⊥平面ABC,BC?平面ABC,
∴MC⊥BC…(4分)
∴BC⊥面MAC
∴BC⊥MA…(6分)
(II)取MB的中点P,连结CP,NP,
则NP∥AM,所以∠PNC是直线AM与CN所成的角,…(8分)
令AN=NB=NC=1,
∴AM=2,NP=1,CP=
| 1 |
| 2 |
在△CPN中,CP=NP=CN=1…(10分)
∴∠PNC=60°…(12分)

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
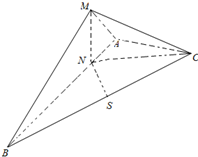 如图,在三棱锥M-ABC中,AB=2AC=2,
如图,在三棱锥M-ABC中,AB=2AC=2, (2007•青岛一模)在三棱锥M-ABC中,CM⊥平面ABC,MA=MB,NA=NB=NC.
(2007•青岛一模)在三棱锥M-ABC中,CM⊥平面ABC,MA=MB,NA=NB=NC.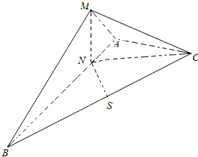 如图,在三棱锥M-ABC中,AB=2AC=2,
如图,在三棱锥M-ABC中,AB=2AC=2,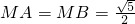 ,AB=4AN,AB⊥AC,平面MAB⊥平面ABC,S为BC中点
,AB=4AN,AB⊥AC,平面MAB⊥平面ABC,S为BC中点 (Ⅱ)若∠AMB=60°,求直线AM与CN所成的角。
(Ⅱ)若∠AMB=60°,求直线AM与CN所成的角。