题目内容
函数 .
.
(I)若f(x)在x=2处取得极值,求p的值;
(II)若f(x)在其定义域内为单调函数求p的取值范围;
(III)若在[1,e]上至少存在一点x0,使得f(x0)>g(x0)成立,求p的取值范围.
解:(I)f′(x)=
∵f(x)在x=2处取得极值,∴f′(2)=0
∴ ,∴p=
,∴p= ;
;
(II)若f(x)在其定义域内为单调函数,则f′(x)≥0或f′(x)≤0恒成立
若f′(x)≥0恒成立,则 在(0,+∞)上恒成立,即
在(0,+∞)上恒成立,即
若f′(x)≤0恒成立,则 在(0,+∞)上恒成立,即
在(0,+∞)上恒成立,即
令 =
=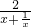
∴x=1时,h(x)max=1;x→0或x→+∞时,h(x)min→0
∴p≤0或p≥1;
(III)∵g(x)在[1,e]上单调递减,∴g(x)的值域为[2,2e].
①若p≥1,由(II)知,f(x)在[1,e]上单调递增,∴f(x)的值域为[0, ]
]
∵在[1,e]上至少存在一点x0,使得f(x0)>g(x0)成立,
∴ ,∴p>
,∴p>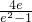 ;
;
②若p≤0,由(II)知,f(x)在[1,e]上单调递减,∴f(x)的值域为[ ,0]
,0]
∵f(x)max=0<2=g(x)min,∴此时不满足题意
③若0<p<1,则 ≤
≤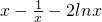 ,函数在[1,e]上单调递增
,函数在[1,e]上单调递增
∴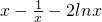 ≤e-
≤e-
∵e- <2=g(x)min,∴此时不满足题意
<2=g(x)min,∴此时不满足题意
综上,p>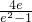 .
.
分析:(I)求导函数,利用f(x)在x=2处取得极值,可得f′(2)=0,从而可求p的值;
(II)若f(x)在其定义域内为单调函数,则f′(x)≥0或f′(x)≤0恒成立,若f′(x)≥0恒成立,则 在(0,+∞)上恒成立,即
在(0,+∞)上恒成立,即 ;若f′(x)≤0恒成立,则
;若f′(x)≤0恒成立,则 在(0,+∞)上恒成立,即
在(0,+∞)上恒成立,即 ,由此可求p的取值范围;
,由此可求p的取值范围;
(III)先确定g(x)的值域为[2,2e].再分类讨论,确定f(x)的值域,利用在[1,e]上至少存在一点x0,使得f(x0)>g(x0)成立,构建不等式,即可求p的取值范围.
点评:本题考查导数知的运用,考查函数的极值与最值,考查函数的单调性,考查分类讨论的数学思想,属于中档题.

∵f(x)在x=2处取得极值,∴f′(2)=0
∴
 ,∴p=
,∴p= ;
;(II)若f(x)在其定义域内为单调函数,则f′(x)≥0或f′(x)≤0恒成立
若f′(x)≥0恒成立,则
 在(0,+∞)上恒成立,即
在(0,+∞)上恒成立,即
若f′(x)≤0恒成立,则
 在(0,+∞)上恒成立,即
在(0,+∞)上恒成立,即
令
 =
=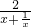
∴x=1时,h(x)max=1;x→0或x→+∞时,h(x)min→0
∴p≤0或p≥1;
(III)∵g(x)在[1,e]上单调递减,∴g(x)的值域为[2,2e].
①若p≥1,由(II)知,f(x)在[1,e]上单调递增,∴f(x)的值域为[0,
 ]
]∵在[1,e]上至少存在一点x0,使得f(x0)>g(x0)成立,
∴
 ,∴p>
,∴p>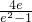 ;
;②若p≤0,由(II)知,f(x)在[1,e]上单调递减,∴f(x)的值域为[
 ,0]
,0]∵f(x)max=0<2=g(x)min,∴此时不满足题意
③若0<p<1,则
 ≤
≤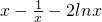 ,函数在[1,e]上单调递增
,函数在[1,e]上单调递增∴
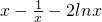 ≤e-
≤e-
∵e-
 <2=g(x)min,∴此时不满足题意
<2=g(x)min,∴此时不满足题意综上,p>
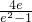 .
.分析:(I)求导函数,利用f(x)在x=2处取得极值,可得f′(2)=0,从而可求p的值;
(II)若f(x)在其定义域内为单调函数,则f′(x)≥0或f′(x)≤0恒成立,若f′(x)≥0恒成立,则
 在(0,+∞)上恒成立,即
在(0,+∞)上恒成立,即 ;若f′(x)≤0恒成立,则
;若f′(x)≤0恒成立,则 在(0,+∞)上恒成立,即
在(0,+∞)上恒成立,即 ,由此可求p的取值范围;
,由此可求p的取值范围;(III)先确定g(x)的值域为[2,2e].再分类讨论,确定f(x)的值域,利用在[1,e]上至少存在一点x0,使得f(x0)>g(x0)成立,构建不等式,即可求p的取值范围.
点评:本题考查导数知的运用,考查函数的极值与最值,考查函数的单调性,考查分类讨论的数学思想,属于中档题.

练习册系列答案
相关题目
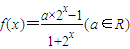 .
. .(I)若f(x)的周期为
.(I)若f(x)的周期为 的值域;(II)若函数f(x)的图象的一条对称轴为
的值域;(II)若函数f(x)的图象的一条对称轴为 的值.
的值.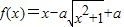 .
.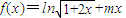 .
.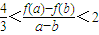 .
.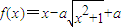 .
.