题目内容
设a>0,函数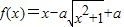 .
.(I)若f(x)在区间(0,1]上是增函数,求a的取值范围;
(Ⅱ)求f(x)在区间(0,1]上的最大值.
【答案】分析:(1)要使f(x)在区间(0,1]上是增函数,只要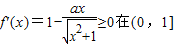 上恒成立,将a参数分离即可求出a的范围;
上恒成立,将a参数分离即可求出a的范围;
(2)欲求f(x)在区间(0,1]上的最大值,即研究函数f(x)在区间(0,1]上单调性,对a进行讨论,求出函数的最值.
解答:解:(I)对函数 .(2分)
.(2分)
要使f(x)在区间(0,1]上是增函数,只要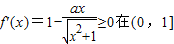 上恒成立,
上恒成立,
即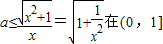 上恒成立(4分)
上恒成立(4分)
因为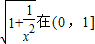 上单调递减,所以
上单调递减,所以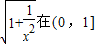 上的最小值是
上的最小值是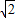 ,
,
注意到a>0,所以a的取值范围是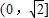 .(6分)
.(6分)
(II)解:①当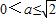 时,由(I)知,f(x)在区间(0,1]上是增函数,
时,由(I)知,f(x)在区间(0,1]上是增函数,
此时f(x)在区间(0,1]上的最大值是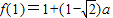 .(8分)
.(8分)
②当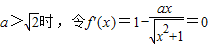 ,
,
解得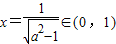 .(10分)
.(10分)
因为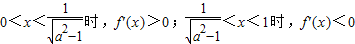 ,
,
所以 上单调递减,
上单调递减,
此时f(x)在区间(0,1]上的最大值是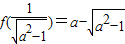 .(13分)
.(13分)
综上,当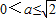 时,f(x)在区间(0,1]上的最大值是
时,f(x)在区间(0,1]上的最大值是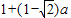 ;
;
当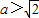 时,f(x)在区间(0,1]上的最大值是
时,f(x)在区间(0,1]上的最大值是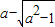 .(14分)
.(14分)
点评:本小题主要考查函数的导数,单调性,极值,最值等基础知识,考查综合利用数学知识分析问题、解决问题的能力,属于中档题.
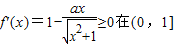 上恒成立,将a参数分离即可求出a的范围;
上恒成立,将a参数分离即可求出a的范围;(2)欲求f(x)在区间(0,1]上的最大值,即研究函数f(x)在区间(0,1]上单调性,对a进行讨论,求出函数的最值.
解答:解:(I)对函数
 .(2分)
.(2分)要使f(x)在区间(0,1]上是增函数,只要
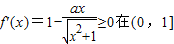 上恒成立,
上恒成立,即
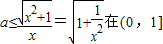 上恒成立(4分)
上恒成立(4分)因为
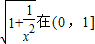 上单调递减,所以
上单调递减,所以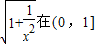 上的最小值是
上的最小值是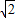 ,
,注意到a>0,所以a的取值范围是
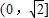 .(6分)
.(6分)(II)解:①当
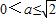 时,由(I)知,f(x)在区间(0,1]上是增函数,
时,由(I)知,f(x)在区间(0,1]上是增函数,此时f(x)在区间(0,1]上的最大值是
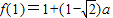 .(8分)
.(8分)②当
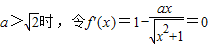 ,
,解得
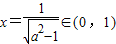 .(10分)
.(10分)因为
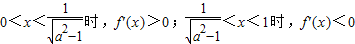 ,
,所以
 上单调递减,
上单调递减,此时f(x)在区间(0,1]上的最大值是
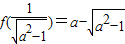 .(13分)
.(13分)综上,当
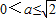 时,f(x)在区间(0,1]上的最大值是
时,f(x)在区间(0,1]上的最大值是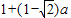 ;
;当
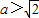 时,f(x)在区间(0,1]上的最大值是
时,f(x)在区间(0,1]上的最大值是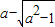 .(14分)
.(14分)点评:本小题主要考查函数的导数,单调性,极值,最值等基础知识,考查综合利用数学知识分析问题、解决问题的能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
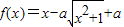 .
.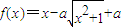 .
.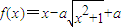 .
.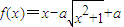 .
.