题目内容
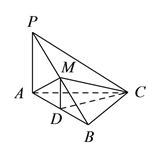
【题目】如图,在三棱锥![]() 中,
中, ![]() ,
, ![]() ,
, ![]() 为
为![]() 的中点,
的中点, ![]() 为
为![]() 的中点,且
的中点,且![]() 为正三角形.
为正三角形.
(![]() )求证:
)求证: ![]() 平面
平面![]() .
.
(![]() )若
)若![]() ,
, ![]() ,求点
,求点![]() 到平面
到平面![]() 的距离.
的距离.

【答案】(1)证明见解析;(2) ![]() .
.
【解析】试题分析:
(1)要证![]() 平面
平面![]() ,只需证明
,只需证明![]() 与平面
与平面![]() 内的两条相交直线
内的两条相交直线![]() 垂直,利用直线与平面垂直的判定定理证明即可;
垂直,利用直线与平面垂直的判定定理证明即可;
(2)解法一:通过![]() ,利用等体积法
,利用等体积法![]() ,即可求解点
,即可求解点![]() 到平面
到平面![]() 的距离;
的距离;
解法二:过点![]() 作直线
作直线![]() 的垂线,角
的垂线,角![]() 的延长线于点
的延长线于点![]() ,证明
,证明![]() 平面
平面![]() ,说明
,说明![]() 为点
为点![]() 到平面
到平面![]() 的距离,一是利用等面积求解,二是利用解直角三角形求解.
的距离,一是利用等面积求解,二是利用解直角三角形求解.
试题解析:
(![]() )
)
证明:在正![]() 中,
中, ![]() 是
是![]() 的中点,
的中点,
∴![]() ,
,
∵![]() 是
是![]() 的中点,
的中点, ![]() 是
是![]() 的中点,
的中点,
∴![]() ,故
,故![]() ,
,
又![]() ,
, ![]() ,
,
![]() ,
, ![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,
,
∵![]() 平面
平面![]() ,
,
∴![]() ,
,
又![]() ,
, ![]() ,
,
![]() ,
, ![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
(![]() )解法
)解法![]() :设点
:设点![]() 到平面
到平面![]() 的距离为
的距离为![]() ,
,
∵![]() ,
, ![]() 是
是![]() 的中点,
的中点,
∴![]() ,
,
∵![]() 为正三角形,
为正三角形,
∴![]() .
.
∵![]() ,
, ![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵ .
.
由(![]() )知
)知![]() ,
,
∴![]() ,
,
在![]() 中,
中, ![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
即![]() ,
,
∴![]() ,
,
故点![]() 到平面
到平面![]() 的距离为
的距离为![]() .
.


练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目
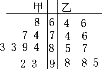
【题目】对某班一次测验成绩进行统计,如下表所示:
分数段 | [40,50) | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
概率 | 0.02 | 0.04 | 0.17 | 0.36 | 0.25 | 0.15 |
(1)求该班成绩在[80,100]内的概率;
(2)求该班成绩在[60,100]内的概率.