题目内容
关于函数 (x∈R)有下列命题:
(x∈R)有下列命题:
①由f(x1)=f(x2)=0可得x1-x2必是π的整数倍;
②y=f(x)的图象可由y=2cos2x的图象向右平移 个单位得到;
个单位得到;
③y=f(x)的图象关于直线 对称;
对称;
④y=f(x)在区间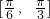 上是减函数.
上是减函数.
其中是假命题的序号有________.
①②③
分析:先把f(x)化为f(x)= .
.
①根据f(x1)=f(x2)=0可得 ,对k讨论即可;
,对k讨论即可;
②把f(x)向右平移 个单位可得
个单位可得 ,再化简比较即可;
,再化简比较即可;
③若y=f(x)的图象关于直线 对称,则必有
对称,则必有 ,否则关于直线
,否则关于直线 不对称;
不对称;
④利用y=sinx在区间 单调递减进行判断即可.
单调递减进行判断即可.
解答:∵f(x)= =
= =
= .
.
①由f(x1)=f(x2)=0可得 =0,
=0,
∴ ,
, .
.
∴2x1-2x2=(k1-k2)π,
∴ .
.
当k=2n(n∈Z)时,x1-x2=nπ,此时x1-x2是π的整数倍;
当k=2n+1,(n∈Z)时, =
= ,此时x1-x2不是π的整数倍;
,此时x1-x2不是π的整数倍;
故①不正确;
②由y=2cos2x的图象向右平移 个单位得到y=
个单位得到y= =2
=2 =
= ≠
≠ ,故②不正确;
,故②不正确;
③ =
= =0≠±2,故y=f(x)的图象关于直线
=0≠±2,故y=f(x)的图象关于直线 不对称,∴③不正确;
不对称,∴③不正确;
④∵ ,∴
,∴ ,∴函数f(x)=
,∴函数f(x)= 在区间
在区间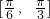 上是减函数,∴④正确.
上是减函数,∴④正确.
综上可知:假命题是①②③.
故答案为①②③.
点评:正确理解函数y=Asin(ωx+φ)的对称性、单调性和平移变换等性质是解题的关键.
分析:先把f(x)化为f(x)=
 .
.①根据f(x1)=f(x2)=0可得
 ,对k讨论即可;
,对k讨论即可;②把f(x)向右平移
 个单位可得
个单位可得 ,再化简比较即可;
,再化简比较即可;③若y=f(x)的图象关于直线
 对称,则必有
对称,则必有 ,否则关于直线
,否则关于直线 不对称;
不对称;④利用y=sinx在区间
 单调递减进行判断即可.
单调递减进行判断即可.解答:∵f(x)=
 =
= =
= .
.①由f(x1)=f(x2)=0可得
 =0,
=0,∴
 ,
, .
.∴2x1-2x2=(k1-k2)π,
∴
 .
.当k=2n(n∈Z)时,x1-x2=nπ,此时x1-x2是π的整数倍;
当k=2n+1,(n∈Z)时,
 =
= ,此时x1-x2不是π的整数倍;
,此时x1-x2不是π的整数倍;故①不正确;
②由y=2cos2x的图象向右平移
 个单位得到y=
个单位得到y= =2
=2 =
= ≠
≠ ,故②不正确;
,故②不正确;③
 =
= =0≠±2,故y=f(x)的图象关于直线
=0≠±2,故y=f(x)的图象关于直线 不对称,∴③不正确;
不对称,∴③不正确;④∵
 ,∴
,∴ ,∴函数f(x)=
,∴函数f(x)= 在区间
在区间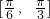 上是减函数,∴④正确.
上是减函数,∴④正确.综上可知:假命题是①②③.
故答案为①②③.
点评:正确理解函数y=Asin(ωx+φ)的对称性、单调性和平移变换等性质是解题的关键.

练习册系列答案
相关题目
 (x∈R)有下列命题:
(x∈R)有下列命题: 个单位得到;
个单位得到; 对称;
对称; 上是减函数.
上是减函数. (x∈R)有下列命题:
(x∈R)有下列命题: 个单位得到;
个单位得到; 对称;
对称; 上是减函数.
上是减函数.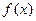 = 4sin
= 4sin (x∈R),有下列命题:来源:高考资源网
(x∈R),有下列命题:来源:高考资源网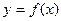 )的表达式可改写为y = 4cos(2x - );
)的表达式可改写为y = 4cos(2x - );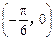 对称;来源:高考资源网
对称;来源:高考资源网