题目内容
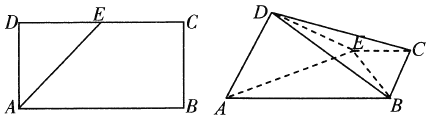
【题目】如图,在多面体![]() 中,四边形
中,四边形![]() 为正方形,
为正方形,![]() ,
,![]() ,
,![]() .
.

(1)证明:平面![]() 平面
平面![]() .
.
(2)若![]() 平面
平面![]() ,二面角
,二面角![]() 为
为![]() ,三棱锥
,三棱锥![]() 的外接球的球心为
的外接球的球心为![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)详见解析;(2)![]() .
.
【解析】
证明![]() 平面
平面![]() 即可证明平面
即可证明平面![]() 平面
平面![]() (2)由题确定二面角
(2)由题确定二面角![]() 的平面角为
的平面角为![]() ,进而推出
,进而推出![]() 为线段
为线段![]() 的中点,以
的中点,以![]() 为坐标原点建立空间直角坐标系
为坐标原点建立空间直角坐标系![]() 由空间向量的线面角公式求解即可
由空间向量的线面角公式求解即可
(1)证明:因为四边形![]() 为正方形,
为正方形,
所以![]() ,
,
又![]() ,
,![]() ,
,
所以![]() 平面
平面![]() .
.
因为![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.
(2)解:由(1)知![]() 平面
平面![]() ,又
,又![]() ,则
,则![]() 平面
平面![]() ,从而
,从而![]() ,
,
又![]() ,所以二面角
,所以二面角![]() 的平面角为
的平面角为![]() .
.
以![]() 为坐标原点建立空间直角坐标系
为坐标原点建立空间直角坐标系![]() ,如图所示,
,如图所示,

则![]() ,
,![]() ,
,![]() .
.
因为三棱锥![]() 的外接球的球心为
的外接球的球心为![]() ,所以
,所以![]() 为线段
为线段![]() 的中点,
的中点,
则![]() 的坐标为
的坐标为![]() ,
,![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,则
,则![]() ,
,
即 令
令![]() ,得
,得![]() .
.
易知平面![]() 的一个法向量为
的一个法向量为![]() ,
,
则![]() .
.
由图可知,二面角![]() 为锐角,
为锐角,
故二面角![]() 的余弦值为
的余弦值为![]() .
.

 教材全解字词句篇系列答案
教材全解字词句篇系列答案【题目】设某校新、老校区之间开车单程所需时间为![]() ,
,![]() 只与道路畅通状况有关,对其容量为
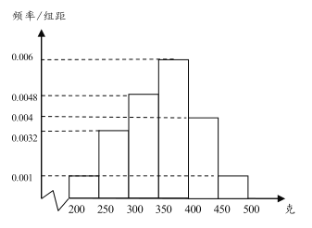
只与道路畅通状况有关,对其容量为![]() 的样本进行统计,结果如图:
的样本进行统计,结果如图:
| 25 | 30 | 35 | 40 |
频数(次) | 20 | 30 | 40 | 10 |
(1)求![]() 的分布列与数学期望
的分布列与数学期望![]() ;
;
(2)刘教授驾车从老校区出发,前往新校区做一个50分钟的讲座,结束后立即返回老校区,求刘教授从离开老校区到返回老校区共用时间不超过120分钟的概率.
【题目】某大学高等数学这学期分别用![]() 两种不同的数学方式试验甲、乙两个大一新班(人数均为
两种不同的数学方式试验甲、乙两个大一新班(人数均为![]() 人,入学数学平均分和优秀率都相同;勤奋程度和自觉性都一样).现随机抽取甲、乙两班各
人,入学数学平均分和优秀率都相同;勤奋程度和自觉性都一样).现随机抽取甲、乙两班各![]() 名的高等数学期末考试成绩,得到茎叶图:
名的高等数学期末考试成绩,得到茎叶图:


(1)学校规定:成绩不得低于85分的为优秀,请填写下面的![]() 列联表,并判断“能否在犯错误率的概率不超过0.025的前提下认为成绩优异与教学方式有关?”
列联表,并判断“能否在犯错误率的概率不超过0.025的前提下认为成绩优异与教学方式有关?”
下面临界值表仅供参考:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(参考方式:![]() ,其中
,其中![]() )
)
(2)现从甲班高等数学成绩不得低于80分的同学中随机抽取两名同学,求成绩为86分的同学至少有一个被抽中的概率.