题目内容
已知各项都为正的等比数列{an}满足a7=a6+2a5,存在两项am,an使得 =4a1,则
=4a1,则 的最小值为________.
的最小值为________.
 =4a1,则
=4a1,则 的最小值为________.
的最小值为________.
由a7=a6+2a5,得a1q6=a1q5+2a1q4,整理有q2-q-2=0,解得q=2或q=-1(与条件中等比数列的各项都为正矛盾,舍去),又由 =4a1,得aman=16
=4a1,得aman=16 ,即
,即 2m+n-2=16
2m+n-2=16 ,即有m+n-2=4,亦即m+n=6,那么
,即有m+n-2=4,亦即m+n=6,那么 =
= (m+n)
(m+n) =
=
 ≥
≥
 =
= ,当且仅当
,当且仅当 ,即n=2m=4时取得最小值
,即n=2m=4时取得最小值
 =4a1,得aman=16
=4a1,得aman=16 ,即
,即 2m+n-2=16
2m+n-2=16 ,即有m+n-2=4,亦即m+n=6,那么
,即有m+n-2=4,亦即m+n=6,那么 =
= (m+n)
(m+n) =
=
 ≥
≥
 =
= ,当且仅当
,当且仅当 ,即n=2m=4时取得最小值
,即n=2m=4时取得最小值

练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目




 ,
, ,…,
,…, ,…是首项为1,公比为-
,…是首项为1,公比为- 的等比数列,则a5等于________.
的等比数列,则a5等于________.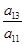 =________.
=________. +
+ ≥2
≥2
 为等比数列,
为等比数列, ,则
,则 .
.