题目内容
(13分)(2011•重庆)设α∈R,f(x)=cosx(asinx﹣cosx)+cos2( ﹣x)满足
﹣x)满足 ,求函数f(x)在
,求函数f(x)在 上的最大值和最小值.
上的最大值和最小值.
 ﹣x)满足
﹣x)满足 ,求函数f(x)在
,求函数f(x)在 上的最大值和最小值.
上的最大值和最小值.最大值是: 2 最小值为: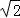
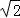
试题分析:利用二倍角公式化简函数f(x),然后
 ,求出a的值,进一步化简为f(x)=2sin(2x﹣
,求出a的值,进一步化简为f(x)=2sin(2x﹣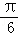 ),然后根据x的范围求出2x﹣
),然后根据x的范围求出2x﹣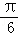 ,的范围,利用单调性求出函数的最大值和最小值.
,的范围,利用单调性求出函数的最大值和最小值.解:f(x)=cosx(asinx﹣cosx)+cos2(
 ﹣x)
﹣x)=asinxcosx﹣cos2x+sin2x
=
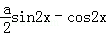
由
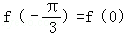 得
得
解得a=2

所以f(x)=2sin(2x﹣
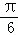 ),
),所以x∈[
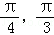 ]时2x﹣
]时2x﹣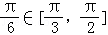 ,f(x)是增函数,
,f(x)是增函数,所以x∈[
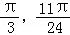 ]时2x﹣
]时2x﹣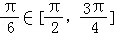 ,f(x)是减函数,
,f(x)是减函数,函数f(x)在
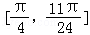 上的最大值是:f(
上的最大值是:f(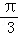 )=2;
)=2;又f(
 )=
)=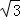 ,f(
,f(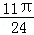 )=
)=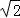 ;
;所以函数f(x)在
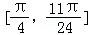 上的最小值为:f(
上的最小值为:f(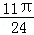 )=
)=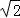 ;
;点评:本题是中档题,考查三角函数的化简,二倍角公式的应用,三角函数的求值,函数的单调性、最值,考查计算能力,常考题型.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
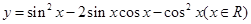 的单调递增区间为 .
的单调递增区间为 .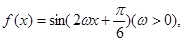 直线
直线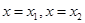 是
是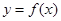 图像的任意两条对称轴,且
图像的任意两条对称轴,且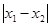 的最小值为
的最小值为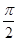 .
.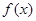 的单调增区间;
的单调增区间;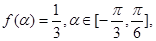 求
求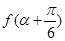 的值;
的值;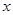 的方程
的方程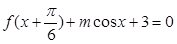 在
在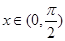 有实数解,求实数
有实数解,求实数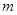 的取值.
的取值.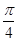 个单位
个单位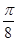 个单位
个单位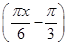 (0≤x≤9)的最大值与最小值之和为( )
(0≤x≤9)的最大值与最小值之和为( )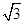
 ,函数
,函数 的图像向右平移
的图像向右平移 个单位后与原图像重合,则
个单位后与原图像重合,则 的最小值是( )
的最小值是( )


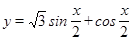 的图像,并说明这个图像是由
的图像,并说明这个图像是由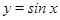 的图像经过怎样的变换得到的.
的图像经过怎样的变换得到的. (0≤x≤9)的最大值与最小值的和为( ).
(0≤x≤9)的最大值与最小值的和为( ).

 cosωx,x∈R,又f(α)=-2,f(β)=0,且|α-β|的最小值为
cosωx,x∈R,又f(α)=-2,f(β)=0,且|α-β|的最小值为 ,则正数ω的值为( )
,则正数ω的值为( )


