题目内容
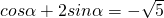，则tan2α=
- A.
- B.
- C.
- D.-2
C
分析：根据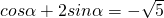，利用辅助角公式，可求sinα=-
，cosα=-
，从而tanα=2，再利用二倍角的正切公式，即可求得结论．
解答：∵，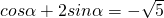
∴
，（其中cosφ=，sinφ=）
∴sin（α+φ）=-1
∴α+φ=
∴α=-φ
∴sinα=-cosφ=-，cosα=-
∴tanα=2
∴tan2α=
=-
故选C．
点评：本题考查二倍角的正切公式，考查辅助角公式的运用，解题的关键是求出tanα的值．
分析：根据
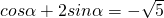，利用辅助角公式，可求sinα=-，cosα=-，从而tanα=2，再利用二倍角的正切公式，即可求得结论．解答：∵
，∴
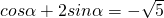，（其中cosφ=，sinφ=）∴sin（α+φ）=-1
∴α+φ=
∴α=-φ
∴sinα=-cosφ=-
，cosα=-∴tanα=2
∴tan2α=
=-故选C．
点评：本题考查二倍角的正切公式，考查辅助角公式的运用，解题的关键是求出tanα的值．
练习册系列答案
世纪百通期末金卷系列答案
相关题目
，则tan2α=
B．
，则tan2α=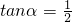
，则tan2α=
的倾斜角为θ，则tan2θ=
