题目内容
已知函数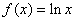 .
.
(I)证明曲线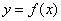 与曲线
与曲线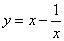 有唯一的公共点;
有唯一的公共点;
(II)设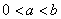 ,比较
,比较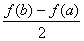 与
与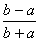 的大小,并说明理由.
的大小,并说明理由.
(1)令 ,则
,则

 在
在 内单调递减,
内单调递减,
又
所以 是函数
是函数 的惟一的零点。所以点
的惟一的零点。所以点 是两曲线惟一的公共点.
是两曲线惟一的公共点.
(2) ,
,
又因为 所以
所以 构造函数
构造函数


 在
在 内单调递增
内单调递增
又当 时,
时,

 时,
时, 即
即
则有 成立。即
成立。即 即
即

练习册系列答案
相关题目
题目内容
已知函数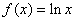 .
.
(I)证明曲线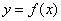 与曲线
与曲线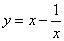 有唯一的公共点;
有唯一的公共点;
(II)设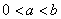 ,比较
,比较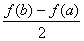 与
与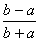 的大小,并说明理由.
的大小,并说明理由.
(1)令 ,则
,则

 在
在 内单调递减,
内单调递减,
又
所以 是函数
是函数 的惟一的零点。所以点
的惟一的零点。所以点 是两曲线惟一的公共点.
是两曲线惟一的公共点.
(2) ,
,
又因为 所以
所以 构造函数
构造函数


 在
在 内单调递增
内单调递增
又当 时,
时,

 时,
时, 即
即
则有 成立。即
成立。即 即
即
