题目内容
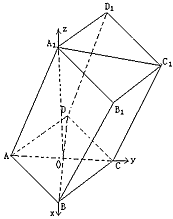
如图,棱柱ABCD-A1B1C1D1的所有棱长都等于2,∠ABC和∠A1B1C1均为60°,平面AA1C1C⊥平面ABCD,
(Ⅰ)求证:BD⊥AA1;
(Ⅱ)求二面角D-AA1-C的余弦值;
(Ⅲ)在直线CC1上是否存在点P,使BP∥平面DA1C1,若存在,求出点P的位置,若不存在,请说明理由。
(Ⅰ)求证:BD⊥AA1;
(Ⅱ)求二面角D-AA1-C的余弦值;
(Ⅲ)在直线CC1上是否存在点P,使BP∥平面DA1C1,若存在,求出点P的位置,若不存在,请说明理由。

|
解:设BD与AC交于O,则BD⊥AC,连结A1O, |
 |

练习册系列答案
相关题目
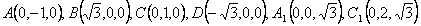 ,
,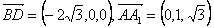 ,
,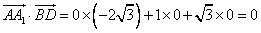 ,
,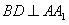 ;
;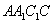 ,
,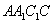 的一个法向量为
的一个法向量为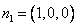 ,
, ,则
,则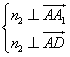 ,
,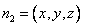 ,则
,则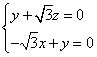 ,
,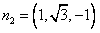 ,
,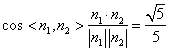 ,
, 。
。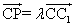 ,P(x,y,z),
,P(x,y,z),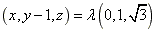 ,
,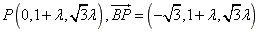 ,
,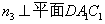 ,则
,则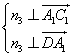 ,
,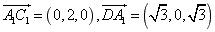 ,
,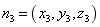 ,则
,则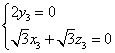 ,取
,取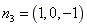 ,
,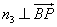 ,即
,即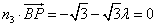 ,
,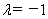 ,即点P在C1C的延长线上,且
,即点P在C1C的延长线上,且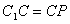 。
。 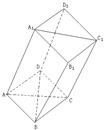 如图,棱柱ABCD-A1B1C1D1的所有棱长都等于2,∠ABC和∠A1B1C1均为60°,平面AA1C1C⊥平面ABCD.
如图,棱柱ABCD-A1B1C1D1的所有棱长都等于2,∠ABC和∠A1B1C1均为60°,平面AA1C1C⊥平面ABCD. 如图四棱柱ABCD-A1B1C1D1的底面ABCD为正方形,侧棱与底边长均为a,且∠A1AD=∠A1AB=60°.
如图四棱柱ABCD-A1B1C1D1的底面ABCD为正方形,侧棱与底边长均为a,且∠A1AD=∠A1AB=60°.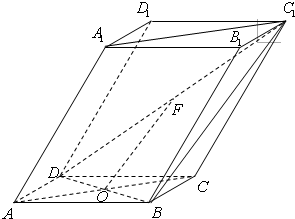 17、如图,棱柱ABCD-A1B1C1D1的底面ABCD为菱形,AC∩BD=O,侧棱AA1⊥BD,点F为DC1的中点.
17、如图,棱柱ABCD-A1B1C1D1的底面ABCD为菱形,AC∩BD=O,侧棱AA1⊥BD,点F为DC1的中点.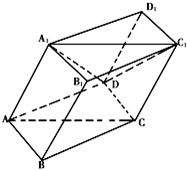 如图,棱柱ABCD-A1B1C1D1的底面ABCD为菱形,平面AA1C1C⊥平面ABCD.?
如图,棱柱ABCD-A1B1C1D1的底面ABCD为菱形,平面AA1C1C⊥平面ABCD.?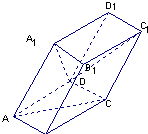 如图,棱柱ABCD-A1B1C1D1的所有棱长都等于2,∠ABC=60°,平面AA1CC1⊥平面ABCD,∠A1AC=60°
如图,棱柱ABCD-A1B1C1D1的所有棱长都等于2,∠ABC=60°,平面AA1CC1⊥平面ABCD,∠A1AC=60°