题目内容
(本小题8分)如图所示,在正三棱柱 中,若
中,若 ,
,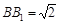 ,
, 是
是 中点。
中点。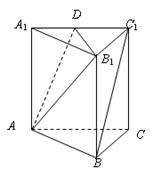
(1)证明: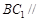 平面
平面 ;
;
(2)求 与
与 所成的角的大小。
所成的角的大小。
(1)见解析;(2) 。
。
解析试题分析:(1)连接 交
交 于点
于点 ,连接
,连接
正三棱柱 的侧面
的侧面 是矩形,所以
是矩形,所以 是
是 的中点
的中点
又 是
是 中点,所以
中点,所以 中
中 …………………… 2分
…………………… 2分 平面
平面 ,
, 平面
平面 ,所以
,所以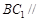 平面
平面 …………4分
…………4分
(2)因为 ,所以
,所以 (或其补角)等于
(或其补角)等于 与
与 所成的角………………… 5分
所成的角………………… 5分
计算得: ,所以
,所以 ,
, ……………7分
……………7分
所以 与
与 所成的角为
所成的角为 ………………8分
………………8分
(用向量法酌情给分)
考点:线面平行的判断定理;异面直线所成的角。
点评:本题是一个典型的异面直线所成的角的问题,解答时也是应用典型的见中点找中点的方法,注意求角的三个环节,一画,二证,三求.

练习册系列答案
相关题目
 中,
中, 为底面圆的两条直径 ,AB交CD于O,且
为底面圆的两条直径 ,AB交CD于O,且 ,
, ,
, 为
为 的中点.
的中点.
 平面
平面 ;
; 与
与 所成角的正切值 .
所成角的正切值 . 中,
中, ,将
,将 沿
沿 折起到
折起到 的位置,使平面
的位置,使平面 平面
平面 .
. 的表面积和体积.
的表面积和体积.
 的底面为直角梯形,
的底面为直角梯形,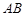 //
//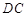 ,
,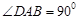 ,
,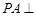 底面
底面 ,且
,且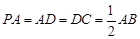 .
.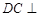 平面
平面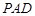 ;
; 的余弦值的大小.
的余弦值的大小.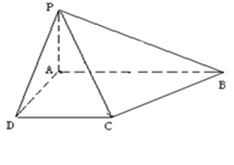
 时,有DN ∥平面AEM,求
时,有DN ∥平面AEM,求  的值;
的值;
 中,
中, ,
, ,点
,点 在棱
在棱 上移动.
上移动.
 //平面
//平面 ;
; ⊥
⊥ ;
; 的体积.
的体积. PD.
PD.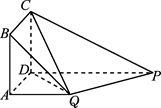
 、
、 分别是正四棱柱
分别是正四棱柱 上、下底面的中
上、下底面的中 是
是 的中点,
的中点, .
. ∥平面
∥平面 ;
; 取何值时,
取何值时, 的重心?
的重心? 