题目内容
已知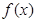 为R上的可导函数,且
为R上的可导函数,且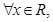 均有
均有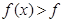 ′(x),则有( )
′(x),则有( )
A.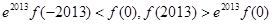 |
B.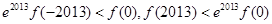 |
C. |
D.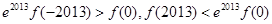 |
D
解析试题分析:因为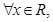 均有
均有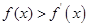 ,即
,即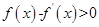 ,构造函数
,构造函数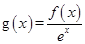 ,则
,则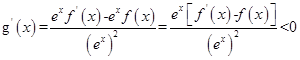 ,所以
,所以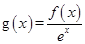 为R上的单调递减函数,所以
为R上的单调递减函数,所以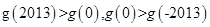 ,即
,即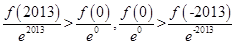 ,所以
,所以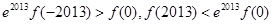 。
。
考点:利用导数研究函数的单调性。
点评:做本题的关键是构造函数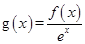 。属于中档题。
。属于中档题。

练习册系列答案
相关题目
若a>b>c,则下列不等式成立的是( )
A.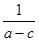 > > | B.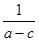 < < | C.ac>bc | D.ac<bc |
设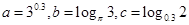 则
则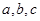 的大小关系是
的大小关系是
A.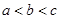 | B.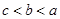 | C.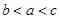 | D. |
设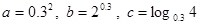 ,则
,则
A.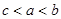 | B.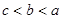 |
C.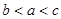 | D.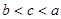 |
不等式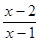 ≥0的解集是( )
≥0的解集是( )
| A.[2,+∞] | B.(-∞,1]∪[2,+∞) |
| C.(-∞,1) | D.(-∞,1)∪[2,+∞) |
下列式子中成立的是( )
A.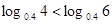 | B.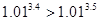 |
C.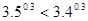 | D.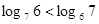 |
不等式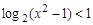 的解集是( )
的解集是( )
A.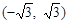 | B.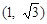 |
C.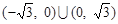 | D.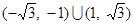 |
三个数 之间的大小关系是( )
之间的大小关系是( )
A.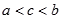 | B. | C. | D.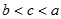 |
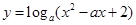 在
在 恒为正,则实数
恒为正,则实数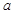 的范围是 .
的范围是 .