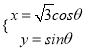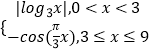题目内容
【题目】已知函数![]() ,在
,在![]() 和
和![]() 处取得极值.
处取得极值.
(1)求函数![]() 的解析式;
的解析式;
(2)求函数![]() 在
在![]() 上的最值.
上的最值.
【答案】(1)![]() (2)函数
(2)函数![]() 在
在![]() 上的最大值为13和最小值为
上的最大值为13和最小值为![]() .
.
【解析】试题分析:(1)由函数的极值与导数的关系,得![]() 和
和![]() 是方程
是方程![]() 的两个实数根,利用根与系数的关系建立关于
的两个实数根,利用根与系数的关系建立关于![]() 的方程组,解之即可得到
的方程组,解之即可得到![]() 的值;
的值;
(2)求导,列表,按利用到时求函数在闭区间上的最值的一般步骤可求函数![]() 在
在![]() 上的最值.
上的最值.
试题解析:
(1)∵![]() ,∴
,∴![]() ,
,
∵在![]() 和
和![]() 处取得极值,∴
处取得极值,∴ ,即
,即 ,。 解得
,。 解得![]() ,
, ![]() .
.
∴![]() .
.
(2)∵![]() ,∴由
,∴由![]() ,解得
,解得![]() 或
或![]() ,
,
当![]() 在
在![]() 上变化时,
上变化时, ![]() 和
和![]() 的变化如下:
的变化如下:
|
|
|
|
|
|
| 1 |
| + |
|
| 0 | + | ||
|
| 单调递增 | 极大值 | 单调递减 | 极小值 | 单调递增 | 4 |
∴由表格可知当![]() 时,函数
时,函数![]() 取得最小值
取得最小值![]() ,在
,在![]() 时,函数取得极大值同时也是最大值
时,函数取得极大值同时也是最大值![]() ,故函数
,故函数![]() 在
在![]() 上的最大值为13和最小值为
上的最大值为13和最小值为![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目